
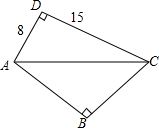
 如图,△ABC为等腰直角三角形,求该直角三角形的面积.
如图,△ABC为等腰直角三角形,求该直角三角形的面积. 分析 先根据勾股定理求出AC的长,再根据△ABC为等腰直角三角形求出AB的长,由三角形的面积公式即可得出结论.
解答 解:∵△ADC中,∠D=90°,AD=8,CD=15,
∴AC=$\sqrt{{AD}^{2}+{CD}^{2}}$=$\sqrt{{8}^{2}+{15}^{2}}$=17.
∵△ABC为等腰直角三角形,
∴AB=AC,2AB2=AC2,即2AB2=289,解得AB=$\frac{17\sqrt{2}}{2}$,
∴S△ABC=$\frac{1}{2}$AB•AC=$\frac{1}{2}$×$\frac{17\sqrt{2}}{2}$×$\frac{17\sqrt{2}}{2}$=$\frac{289}{4}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com