
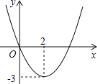
【题目】从图中的二次函数y=ax2+bx+c图象中,观察得出了下面的五条信息:
①b>0 ②c=0;③函数的最小值为﹣3;④a﹣b+c>0;⑤当x1<x2<2时,y1>y2.
(1)你认为其中正确的有哪几个?(写出编号)
(2)根据正确的条件请求出函数解析式.

【答案】![]() ②③④⑤;
②③④⑤;![]()
![]() .
.
【解析】
(1)根据开口方向①;根据抛物线与y轴的交点判断②;根据抛物线顶点坐标及开口方向判断③;观察当x<0时,图象是否在x轴上方,判断④;在0<x1<x2<2时,函数的增减性判断⑤.
(2)利用顶点式求出二次函数的解析式即可.
![]() 根据图象可知:
根据图象可知:
①∵该函数图象的开口向上,∴![]() ,∴
,∴![]() ,(此时
,(此时![]() ,
,![]() 异号)故此选项错误;
异号)故此选项错误;
②![]() 时,可
时,可![]() ,故此选项正确;
,故此选项正确;
③利用函数顶点坐标,函数的最小值为![]() ,故此选项正确;
,故此选项正确;
④根据图象知,当![]() 时,图象是在
时,图象是在![]() 轴上方,∴
轴上方,∴![]() ;即
;即![]() ,故此选项正确;
,故此选项正确;
⑤当![]() 时函数为减函数,
时函数为减函数,![]() 时,
时,![]() ,故此选项正确.
,故此选项正确.
故正确的有:②③④⑤,
![]() ∵函数的顶点坐标为:
∵函数的顶点坐标为:![]() ,
,
∴二次函数的解析式为:![]() ,
,
将![]() 代入求出即可:
代入求出即可:
![]() ,
,
∴函数解析式为:![]() .
.


科目:初中数学 来源: 题型:
【题目】等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、点B分别是y轴、x轴上两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;

(1)如图(1),已知C点的横坐标为-1,直接写出点A的坐标;
(2)如图(2), 当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
(3)如图(3), 若点A在x轴上,且A(-4,0),点B在y轴的正半轴上运动时,分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC,连结CD交y轴于点P,问当点B在y轴的正半轴上运动时,BP的长度是否变化?若变化请说明理由,若不变化,请求出BP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
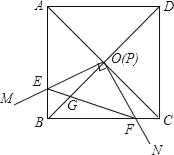
【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G.
(1)求四边形OEBF的面积;
(2)求证:OGBD=EF2;
(3)在旋转过程中,当△BEF与△COF的面积之和最大时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,点D是弧BC的中点,PD切⊙O于点D.
(1)求证:DP⊥AP;
(2)若PD=![]() ,PC=1,求图中阴影部分的面积.(结果保留π)
,PC=1,求图中阴影部分的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在边
在边![]() 上,
上,![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() 是等边三角形,边
是等边三角形,边![]() 交边
交边![]() 于点
于点![]() ,边
,边![]() 交边
交边![]() 于点
于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 当
当![]() 为何值时,以
为何值时,以![]() 为圆心,以
为圆心,以![]() 为半径的圆与
为半径的圆与![]() 相切?
相切?
![]() 设
设![]() ,五边形
,五边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数解析式(要求写出自变量
之间的函数解析式(要求写出自变量![]() 的取值范围);当
的取值范围);当![]() 为何值时,
为何值时,![]() 有最大值?并求
有最大值?并求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在边BC,AC,AB上,且BD=CE,DC=BF,连结DE,EF,DF,∠1=60°

(1)求证:△BDF≌△CED.
(2)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE∥OC交y轴于点E,已知AO=m,BO=n,且m、n满足n2﹣8n+16+|n﹣2m|=0.

(1)求A、B两点的坐标;
(2)若点D为AB中点,求OE的长;
(3)如图2,若点P(x,﹣2x+4)为直线AB在x轴下方的一点,点E是y轴的正半轴上一动点,以E为直角顶点作等腰直角△PEF,使点F在第一象限,且F点的横、纵坐标始终相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止.

(1)用画树状图或列表法求乙获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com