
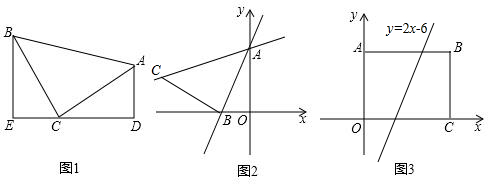
分析 (1)由条件可求得∠EBC=∠ACD,利用AAS可证明△BEC≌△CDA;
(2)①过C作CD⊥x轴于点D,由直线解析式可求得A、B的坐标,利用模型结论可得CE=BO,BE=AO,从而可求得C点坐标,利用待定系数法可求得直线AC的解析式;②分三种情况考虑:如图2所示,当∠ADP=90°时,AD=PD,设D点坐标为(x,2x-6),利用三角形全等得到x+6-(2x-6)=8,得x=4,易得D点坐标;如图3所示,当∠APD=90°时,AP=PD,设点P的坐标为(8,m),表示出D点坐标为(14-m,m+8),列出关于m的方程,求出m的值,即可确定出D点坐标;如图4所示,当∠ADP=90°时,AD=PD时,同理求出D的坐标.
解答 解:
(1)∵∠ACB=90°,
∴∠EBC+∠BCE=∠BCE+∠ACD=90°,
∴∠EBC=∠ACD,
在△BEC和△CDA中
$\left\{\begin{array}{l}{∠EBC=∠ACD}\\{∠E=∠D}\\{BC=AC}\end{array}\right.$
∴△BEC≌△CDA(AAS);
(2)①如图1,过C作CD⊥x轴于点D,
在y=$\frac{4}{3}$x+4中,令y=0可求得x=-3,令x=0可求得y=4,
∴OA=4,OB=3,
同(1)可证得△CDB≌△BAO,
∴CD=BO=3,BD=AO=4,
∴OD=4+3=7,
∴C(-7,3),且A(0,4),
设直线AC解析式为y=kx+4,把C点坐标代入可得-7k+4=3,解得k=$\frac{1}{7}$,
∴直线AC解析式为y=$\frac{1}{7}$x+4;
②如图2,当∠ADP=90°时,AD=PD,易得D点坐标(4,2);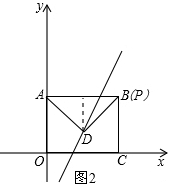
如图3,当∠APD=90°时,AP=PD,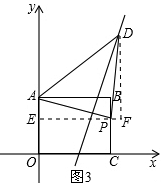
设点P的坐标为(8,m),则D点坐标为(14-m,m+8),由m+8=2(14-m)-6,得m=$\frac{14}{3}$,
∴D点坐标($\frac{28}{3}$,$\frac{38}{3}$);
如图4,当∠ADP=90°时,AD=PD时,同理可求得D点坐标($\frac{20}{3}$,$\frac{22}{3}$),
综上可知满足条件的点D的坐标分别为(4,2)或($\frac{28}{3}$,$\frac{38}{3}$)或($\frac{20}{3}$,$\frac{22}{3}$).
点评 本题为一次函数的综合应用,涉及全等三角形的判定与性质、等腰直角三角形的性质、旋转的性质、分类讨论及数形结合的思想.本题第二问注意考虑问题要全面,做到不重不漏.本题考查知识点较多,综合性较强,难度较大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
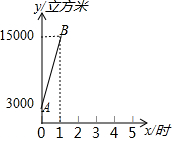 为节约能源,某市众多车主响应号召,将燃油汽车改装为天然气汽车.某日上午7:00-8:00,燃气公司给该市城西加气站的储气罐加气,8:00 加气站开始为前来的车辆加气.储气罐内的天然气总量y(立方米)随加气时间x(时)的变化而变化.
为节约能源,某市众多车主响应号召,将燃油汽车改装为天然气汽车.某日上午7:00-8:00,燃气公司给该市城西加气站的储气罐加气,8:00 加气站开始为前来的车辆加气.储气罐内的天然气总量y(立方米)随加气时间x(时)的变化而变化.| 时刻 | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 |
| y(立方米) | 15000 | 7500 | 5000 | 3750 | 3000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某学校为了加固一篮球架,在下面焊接了一根钢筋撑杆AC,它与水平的钢板箱体成60°的夹角,且AB=0.5m.原有的上撑杆DE=1.6m,且∠BDE=135°.
如图,某学校为了加固一篮球架,在下面焊接了一根钢筋撑杆AC,它与水平的钢板箱体成60°的夹角,且AB=0.5m.原有的上撑杆DE=1.6m,且∠BDE=135°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
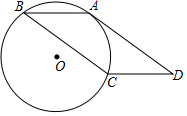 如图,?ABCD的边AD与经过A,B,C三点的⊙O相切,sin∠D=$\frac{5}{13}$,AD=24,则⊙O的半径为$\frac{169}{10}$.
如图,?ABCD的边AD与经过A,B,C三点的⊙O相切,sin∠D=$\frac{5}{13}$,AD=24,则⊙O的半径为$\frac{169}{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 运动会上,甲、乙、丙三位同学进行跳绳比赛,通过“手心手背”游戏决定谁先跳,规则如下:三个人同时各用一只手随机出示手心或手背,若其中有一个人的手势与另外两个不同,则此人先进行比赛,若三个人手势相同,则重新决定,那么通过一次“手心手背”游戏,甲同学先跳绳的概率是多少?
运动会上,甲、乙、丙三位同学进行跳绳比赛,通过“手心手背”游戏决定谁先跳,规则如下:三个人同时各用一只手随机出示手心或手背,若其中有一个人的手势与另外两个不同,则此人先进行比赛,若三个人手势相同,则重新决定,那么通过一次“手心手背”游戏,甲同学先跳绳的概率是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,∠ABC=60°,点E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=$\sqrt{5}$.
如图,在?ABCD中,∠ABC=60°,点E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com