
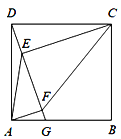
【题目】如图,在正方形ABCD中,点G在边AB上(不与点A,B重合),连接DG,作CE⊥DG于点E,AF⊥DG于点F,连接AE,CF.
(1)求证:DE=AF;
(2)若![]() 设
设![]() ,求
,求![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A(1,2),B(3,2),连接AB.若对于平面内一点P,线段AB上都存在点Q,使得PQ≤2,则称点P是线段AB的“影子”.
(1)在点C(0,1),D(2,![]() ),E(4,5)中,线段AB的”影子”是 .
),E(4,5)中,线段AB的”影子”是 .
(2)若点M(m,n)在直线y=-x+2上,且不是线段AB的“影子”,求m的取值范围.
(3)若直线y=![]() x+b上存在线段AB的“影子”,求b的取值范围以及“影子”构成的区域面积.
x+b上存在线段AB的“影子”,求b的取值范围以及“影子”构成的区域面积.
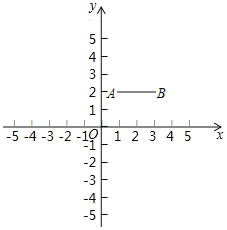
查看答案和解析>>
科目:初中数学 来源: 题型:
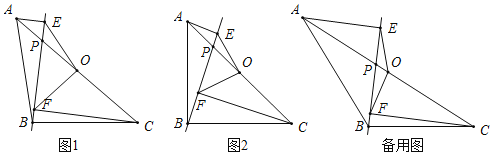
【题目】在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由
(3)若|CF﹣AE|=2,EF=2![]() ,当△POF为等腰三角形时,请直接写出线段OP的长.
,当△POF为等腰三角形时,请直接写出线段OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
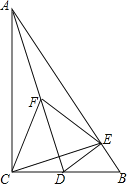
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.
(1)连接AD,取AD中点F,连接CF,CE,FE,判断△CEF的形状并说明理由
(2)若BD=![]() CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.
CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
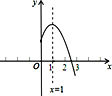
【题目】如图是二次函数![]() (a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2 ,0)和(3 ,0)之间,对称轴是x=1.对于下列结论:① ab<0;② 2a+b=0;③ 3a+c>0;④a+b≥m(am+b)(m为实数);⑤ 当-1<x<3时,y>0. 其中正确结论的个数为( )
(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2 ,0)和(3 ,0)之间,对称轴是x=1.对于下列结论:① ab<0;② 2a+b=0;③ 3a+c>0;④a+b≥m(am+b)(m为实数);⑤ 当-1<x<3时,y>0. 其中正确结论的个数为( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
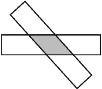
【题目】如图,剪两张对边平行且宽度相等的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠ABC=∠ADC,∠BAD=∠BCD B. AB=BC
C. AB=CD,AD=BC D. ∠DAB+∠BCD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是( )
A. 8B. 10C. 10.4D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AC是直径,弦BD=BA,EB⊥DC,交DC的延长线于点E.
(1)求证:BE是⊙O的切线;
(2)当sin∠BCE=![]() ,AB=3时,求AD的长.
,AB=3时,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】田忌赛马的故事为我们所熟知.小亮与小齐学习概率初步知识后设计了如下游戏:小亮手中有方块l0、8、6三张扑克牌,小齐手中有方块9、7、5三张扑克牌.每人从各自手中取一张牌进行比较,数字大的为本“局”获胜,每次取的牌不能放回.
(1)若每人随机取手中的一张牌进行比赛,求小齐本“局”获胜的概率;
(2)若比赛采用三局两胜制,即胜2局或3局者为本次比赛获胜者.当小亮的三张牌出牌顺序为先出6,再出8,最后出l0时,小齐随机出牌应对,求小齐本次比赛获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com