
【题目】如图,在△PAB中,M.N是AB上两点,△PMN是等边三角形,∠APM=∠B.
(1)求证:∠A=∠BPN;
(2)求证:MN2=AM·BN;
(3)若AP=![]() ,AM=1,求线段MN,PB的长.
,AM=1,求线段MN,PB的长.
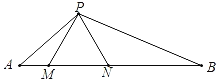
【答案】(1)证明见解析;(2)见解析;(3)MN=2,![]()
【解析】
(1)利用等边三角形的性质可证得∠AMP=∠PNB=![]() ,又∠APM=∠B,可证得△APM∽△PBN,从而证明了∠A=∠BPN;
,又∠APM=∠B,可证得△APM∽△PBN,从而证明了∠A=∠BPN;
(2)由(1)的结论△APM∽△PBN得到![]() ,根据等量代换可证得结论;
,根据等量代换可证得结论;
(3)容易证明△APM∽△ABP,由其对应边成比例及已知,求得![]() ,设MN=x,根据(2)的结论构建方程,求得等边三角形的边长,再根据相似三角形对应边成比例求得最后答案.
,设MN=x,根据(2)的结论构建方程,求得等边三角形的边长,再根据相似三角形对应边成比例求得最后答案.
(1)证明:∵△PMN是等边三角形,
∴∠PMN=∠PNM=60°,
∴∠AMP=∠PNB=120°,
∵∠APM=∠B,
∴△APM∽△PBN,
∠A=∠BPN;
(2)解:∵∠APM=∠B,∠A=∠BPN,
∴△APM∽△PBN,
∴![]() ,即PM·PN=AM·BN,
,即PM·PN=AM·BN,
∵MN=PM=PN,
∴MN 2=AMBN;
(3)解:∵∠A=∠A,∠APM=∠B,
∴△APM∽△ABP,
∴![]() ,
,
∴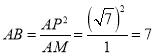 ,
,
设MN=x,则PM=MN=x,BN=6﹣x,
∵MN 2=AMBN,
∴x2=1×(6﹣x),
解得x1=2,x2=﹣3(舍去),
∴PM=MN=2,
∵![]() ,
,
∴![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读并解答:
①方程x2﹣2x+1=0的根是![]() ,则有
,则有![]() .
.
②方程2x2﹣x﹣2=0的根是![]() =
=![]() ,
,![]() =
=![]() ,则有
,则有![]() ,
,![]() .
.
③方程3x2+4x﹣7=0的根是![]() ,
,![]() ,则有
,则有![]() ,
,![]() .
.
(1)根据以上①②③请你猜想:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根为![]() ,那么
,那么![]() 与系数a、b、c有什么关系?请写出你的猜想并证明你的猜想;
与系数a、b、c有什么关系?请写出你的猜想并证明你的猜想;
(2)利用你的猜想结论,解决下面的问题:
已知关于x的方程x2+(2k+1)x+k2﹣2=0有实数根![]() ,且
,且![]() ,求k的值
,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2﹣
x2﹣![]() x﹣3交x轴于A,B两点(点A在点B的左侧),交y轴于点C
x﹣3交x轴于A,B两点(点A在点B的左侧),交y轴于点C
(1)求直线AC的解析式;
(2)点P是直线AC上方抛物线上的一动点(不与点A,点C重合),过点P作PD⊥x轴交AC于点D,求PD的最大值;
(3)将△BOC沿直线BC平移,点B平移后的对应点为点B′,点O平移后的对应点为点O′,点C平移后的对应点为点C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,求出所有符合条件的点S的坐标.
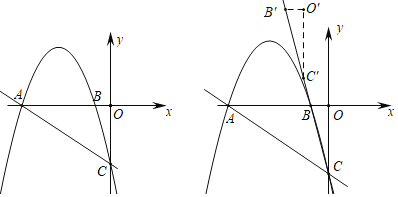
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN与x轴、y轴分别交于A、C两点,分别过A、C两点作x轴、y轴的垂线相交于B点,且OA、OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.
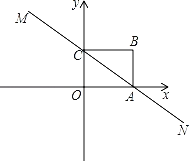
(1)求A、C两点的坐标.
(2)求直线MN的表达式.
(3)在直线MN上存在点P,使以点P、B、C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
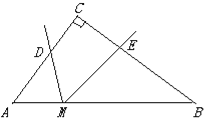
【题目】如图,在Rt△ABC中,已知AC=3,BC=4,点M是AB边上的一个动点,∠DME的两边与折线A—C—B分别交于点D和点E(点E在点D的右边),且∠DME=∠A,若能使以点D,E,M为顶点的三角形与△ABC相似的点D有三个,则AM的长度x的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
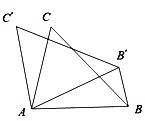
【题目】如图,在△ABC中,∠BAC=75°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C',连接BB',若BB'∥AC',则∠BAC′ 的度数是______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com