
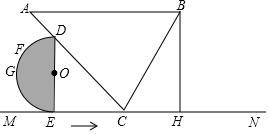
 ��ͼ����A=45�㣬��ABC=60�㣬AB��MN��BH��MN�ڵ�H��BH=8����C��MN�ϣ���D��AC�ϣ�DE��MN�ڵ�E����Բ��Բ��Ϊ��O��ֱ��DE=6��GΪ$\widehat{DE}$���е㣬F��$\widehat{DE}$�ϵĶ��㣮
��ͼ����A=45�㣬��ABC=60�㣬AB��MN��BH��MN�ڵ�H��BH=8����C��MN�ϣ���D��AC�ϣ�DE��MN�ڵ�E����Բ��Բ��Ϊ��O��ֱ��DE=6��GΪ$\widehat{DE}$���е㣬F��$\widehat{DE}$�ϵĶ��㣮���� ���֣��ٵ�F��E�غ�ʱ��CF����СֵΪCE�ij�=6���ڵ�CF����Բ��ʱ��CF�ij����
̽������1��������������ͼ2�У�����G����AC����ʱ����E��C�غϣ�����OG����Բ���ABC�غϲ��ֵ����=��OCG�����+����ODG�������
����ͼ3�У�����G����BC�ϣ��ص����ֵ����=����OGS�����-��OGS�������
��2����E��H�غ�ʱ��BH=8��OE=3��BO=5����BC����Բ��R��T��OP��RT�ڵ�P����PT=PR�����RT�ij����ɣ�
��3������ͼ5�У�����Բ��AC����ʱ�����е�ΪK����CK=CE����KU��DE��U������CE=LE-LC�����LE��LC���ɣ�
����ͼ6�У�����Բ��BC����ʱ�����е�ΪW������OW����CE=CW����Rt��COE�У���ֱ�������μ��ɣ�
��� �⣺���֣���ͼ1�У�
�ٵ�F��E�غ�ʱ��CF����СֵΪCE�ij�=6��
�ڵ�CF����Բ��ʱ��CF�ij����
���ֵ=OC+OF=$\sqrt{{3}^{2}+{6}^{2}}$+3=3$\sqrt{5}$+3��
�ʴ�Ϊ6��3$\sqrt{5}$+3��
̽������1����ͼ2�У�����G����AC����ʱ����E��C�غϣ�����OG��
��GΪ$\widehat{DE}$���е㣬���DOG=��GOC=90�㣬��Բ���ABC�غϲ��ֵ����$\frac{1}{2}$•$\frac{1}{2}$•��•32+$\frac{1}{2}$•3•3=$\frac{9}{4}$��+$\frac{9}{2}$��
��ͼ3�У�����G����BC�ϣ�
��OG��MN��
���BGO=��BCE=60�㣬��BC����Բ��һ����ΪS������OS��
��OS=OG��
���OSG�ǵȱ������Σ�
���Բ���ABC�ص����ֵ����Ϊ$\frac{60}{360}$•��•32-$\frac{\sqrt{3}}{4}$��32=$\frac{3}{2}$��-$\frac{9\sqrt{3}}{4}$��
��2����E��H�غ�ʱ��BH=8��OE=3��BO=5����BC����Բ��R��T��OP��RT�ڵ�P����PT=PR��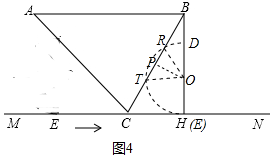
�ߡ�CBE=30�㣬
��OP=$\frac{5}{2}$��
����OR����RP=$\sqrt{{3}^{2}-��\frac{5}{2}��^{2}}$=$\frac{\sqrt{11}}{2}$��
��RT=2PR=$\sqrt{11}$��
��3������ͼ5�У�����Բ��AC����ʱ�����е�ΪK����CK=CE����KU��DE��U��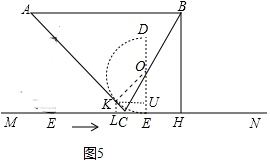
�ߡ�KOE=45�㣬OK=3��
��KU=OU=$\frac{3}{2}$$\sqrt{2}$��EU=3-$\frac{3}{2}\sqrt{2}$��
��KL��MN��L���ɵ�KL=EU��
�ߡ�KCL=45�㣬��LC=KL=EU��
��CE=OU-EU=3$\sqrt{2}$-3��
����ͼ6�У�����Բ��BC����ʱ�����е�ΪW������OW����CE=CW��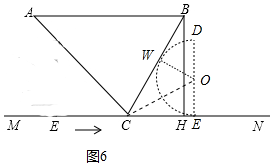
��OW=OE��
���OCE=��OCM=30�㣬
��OE=3��
��tan30��=$\frac{3}{OE}$��
��CE=3$\sqrt{3}$��
���� ���⿼��Բ�ۺ��⡢ƽ�Ʊ任��ֱ����Բ��λ�ù�ϵ����ֱ�������Ρ����ɶ�����֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�����˼�����⣬ѧ�����ӳ��ø����ߣ�����ֱ�������ν�����⣬�����п�ѹ���⣮


 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д� �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
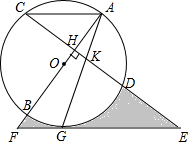 ��ͼ��AB�ǡ�O��ֱ������CD��AB��H��GΪ��O��һ�㣬AG��CD��K��EΪCD�ӳ�����һ�㣬��EK=EG��EG���ӳ��߽�AB���ӳ�����F��
��ͼ��AB�ǡ�O��ֱ������CD��AB��H��GΪ��O��һ�㣬AG��CD��K��EΪCD�ӳ�����һ�㣬��EK=EG��EG���ӳ��߽�AB���ӳ�����F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
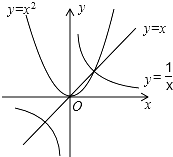 �����������⼰����y=x��y=x2��y=$\frac{1}{x}$��ͼ����ͼ��ʾ��
�����������⼰����y=x��y=x2��y=$\frac{1}{x}$��ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
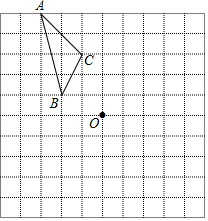 ��ͼ���ڱ߳�Ϊ1����λ���ȵ�С�����������У������ˡ�ABC�������������ߵĽ��㣩��
��ͼ���ڱ߳�Ϊ1����λ���ȵ�С�����������У������ˡ�ABC�������������ߵĽ��㣩���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com