
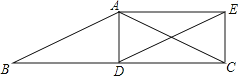
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.
(1)求证:△ACD≌△EDC;
(2)若点D是BC中点,说明四边形ADCE是矩形.
【答案】(1)证明过程见解析;(2)证明过程见解析.
【解析】(1)根据平行四边形的性质、等腰三角形的性质,利用全等三角形的判定定理SAS可以证得△ADC≌△ECD;
(2)利用等腰三角形的“三合一”性质推知AD⊥BC,即∠ADC=90°;由平行四边形的判定定理(对边平行且相等是四边形是平行四边形)证得四边形ADCE是平行四边形,所以有一个角是直角的平行四边形是矩形.
证明:(1)∵四边形ABDE是平行四边形
∴AB∥DE,AB=DE;∴∠B=∠EDC;
又∵AB=AC,∴AC=DE,∠B=∠ACB,
∴∠EDC=∠ACD
∴△ADC≌△ECD(SAS);
(2)∵四边形ABDE是平行四边形
∴BD∥AE,BD=AE,∴AE∥CD;
又∵BD=CD,∴AE=CD(等量代换)
∴四边形ADCE是平行四边形;
在△ABC中,
AB=AC,BD=CD,
∴AD⊥BC,
∴∠ADC=90°,
∴四边形ADCE是矩形.


科目:初中数学 来源: 题型:
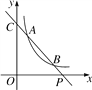
【题目】如图,已知直线y=ax+b与双曲线y=![]() (x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
(1)若A,B两点的坐标分别为(1,3),(3,y2),求点P的坐标;
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点P为∠MON的平分线上一点,以P点为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA·OB=OP2,我们就把∠APB叫作∠MON的智慧角.
(1)如图②,已知∠MON=90°,点P为∠MON的平分线上一点,以点P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°,求证:∠APB是∠MON的智慧角;
(2)如图①,已知∠MON=α(0°<α<90°),OP=2,若∠APB是∠MON的智慧角,连接AB,用含α的式子分别表示∠APB的度数和△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①三角形的外角大于内角;②各条边都相等,各个角都相等的多边形是正多边形;③三角形的三条高相交于一点;④如果a>b,那么m2a>m2b,其中说法正确的有( ).
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
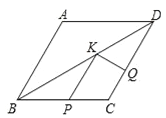
【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
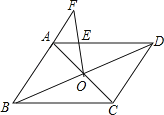
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,过点O与AD上的一点E作直线OE,交BA的延长线于点F.若AD=4,DC=3,AF=2,则AE的长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下问题,不适合使用全面调查的是( )
A. 对旅客上飞机前的安检B. 航天飞机升空前的安全检查
C. 了解全班学生的体重D. 了解广州市中学生每周使用手机所用的时间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com