
已知A,B,C,D是⊙O上的四个点.
(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.



科目:初中数学 来源: 题型:
如图,已知△ABC中,AB=AC,点D、E在BC上,
要使△ABD≌△ACE,则只需添加一个适当的条件:
________________.(只填一个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,抛物线与x轴交于点A(﹣1,0)和点B(1,0),直线y=2x﹣1与y轴交于点C,与抛物线交于点C、D.
(1)求抛物线的解析式;
(2)求点A到直线CD的距离;
(3)平移抛物线,使抛物线的顶点P在直线CD上,抛物线与直线CD的另一个交点为Q,点G在y轴正半轴上,当以G、P、Q三点为顶点的三角形为等腰直角三角形时,求出所有符合条件的G点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
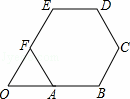
如图,正六边形ABCDEF的边长为2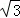 ,延长BA,EF交于点O.以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,则直线DF与直线AE的交点坐标是( ).
,延长BA,EF交于点O.以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,则直线DF与直线AE的交点坐标是( ).


查看答案和解析>>
科目:初中数学 来源: 题型:
用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )
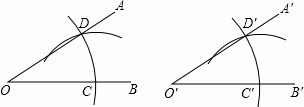
A. (SAS) B. (SSS) C. (ASA) D. (AAS)
查看答案和解析>>
科目:初中数学 来源: 题型:
若a=(-3)13 -(-3)14,b=(-0.6)12 -(-0.6)14,c=(-1.5)11 -(-1.5)13,则下列有关a、b、c的大
小关系,何者正确? (A) a > b > c (B) a > c > b (C) b > c > a (D) c > b > a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com