
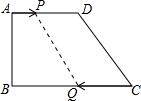
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.分析 (1)四边形PQCD为矩形,即AP=BQ,列出等式,求解即可;
(2)四边形PQCD为平行四边形,即CQ=PD,列出等式求解;
解答 解:(1)由题意知AP=t,CQ=2t,所以BQ=21-2t,
∵AD∥BC,
∴AP∥BQ,
又∵∠B=90°,
∴要使四边形ABQP为矩形,只需满足AP=BQ,
即:t=21-2t,
解得t=7,
∴当t=7s时,四边形ABQP为矩形;
(2)解:由题意知:AP=t,QC=2t,PD=18-t,当PD=QC时,四边形PQCD为平形四边形,
即18-t=2t,
∴t=6,
∴当t=6时,四边形PQCD为平形四边形.
点评 此题主要考查了矩形、平行四边形、等腰梯形的判定与性质应用,要求学生掌握对各种图形的认识,同时学会数形结合的数学解题思想.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:填空题
 如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{5\sqrt{3}+12}{80}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{5\sqrt{3}+12}{80}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A,B在反比例函数y=$\frac{k}{x}$(x>0)的图象中,AC⊥x轴于点C,BD⊥y轴于点D,交AC于点F,连接AB,CD,若图中的阴影部分的面积和为5,且AE=2CE,则k的值为( )
如图,点A,B在反比例函数y=$\frac{k}{x}$(x>0)的图象中,AC⊥x轴于点C,BD⊥y轴于点D,交AC于点F,连接AB,CD,若图中的阴影部分的面积和为5,且AE=2CE,则k的值为( )| A. | 5 | B. | 6 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示的函数图象反映的过程是:小明从家去书店看一会儿书,又去学校取封信后马上回家,其中x表示时间(单位:小时),y表示小明离家的距离(单位:千米),则小明从学校回家的平均速度为6千米∕小时.
如图所示的函数图象反映的过程是:小明从家去书店看一会儿书,又去学校取封信后马上回家,其中x表示时间(单位:小时),y表示小明离家的距离(单位:千米),则小明从学校回家的平均速度为6千米∕小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com