
如图,小岛A在港口P的南偏西4 5°方向,距离港口81海里处,甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口.现两船同时出发.
5°方向,距离港口81海里处,甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口.现两船同时出发.
(1)出发后几小时两船与港口P的距离相等?
(2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)(参考数据: ≈1.41,
≈1.41,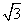 ≈1.73)
≈1.73)

解:(1)设出发后xh两船与港口P的距离相等,
根据题意,得81-9x=18x,解这个方程,得x=3,
∴出发后3h两船与港口P的距离相等.
(2)设出发后xh乙船在甲船的正东方向,
此时甲、乙两船的 位置分别在点C,D处,
位置分别在点C,D处,
连接CD,过点P作PE⊥CD,垂足为E,则点E在点P的正南方向.
在Rt△CEP中,∠CPE=45°,
 ∴PE=PC·cos45°,
∴PE=PC·cos45°,
在Rt△PED中,∠EPD=6 0
0 °
°
∴PE=PD·cos60°,
∴PC·cos45°=PD·cos60°,
∴(81-9x)·cos45°=18x·cos60°,
解这个方程,得x≈3.7,
∴出发后约3.7h乙船在甲船的正东方向.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
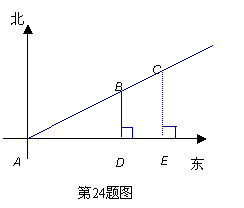
如图所示,一条渔船某时刻在位置A观测灯塔B、C(灯塔B距离A处较近),两个灯塔恰好在北偏东65°45′的方向上,渔船向正东方向航行1小时45分钟之后到达D点,观测到灯塔B恰好在正北方向上,在图中作CE⊥AD.已知两个灯塔之间的距离是12海里,渔船的速度是16海里/时,又知在灯塔C周围18 .6海里内有暗礁,问这条渔船按原来的方向续航行,有没有触礁的危
.6海里内有暗礁,问这条渔船按原来的方向续航行,有没有触礁的危 险?
险?
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com