
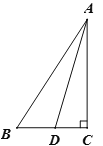
【题目】如图,Rt△ ABC中,∠ACB=90°,AD平分∠BAC, 作AD的垂直平分线EF交AD于点E,交BC的延长线于点F,交AB于点G,交AC于点H.
(1)依题意补全图形;
(2)求证:∠BAD=∠BFG;
(3)试猜想AB,FB和FD之间的数量关系并进行证明.
【答案】(1)补图见解析;(2)证明见解析;(3)![]() ,证明见解析.
,证明见解析.
【解析】
(1)根据题意补全图形;
(2)根据角平分线的定义得到∠BAD=∠CAD.在Rt△AEH和Rt△CFH中,根据三角形内角和定理得到∠CFH=∠CAD,等量代换即可得到结论;
(3)由线段垂直平分线的性质得到AF=FD,通过证明∠BAF=90°.在Rt△BAF中,利用勾股定理即可得到结论.
(1)补全图形如图;
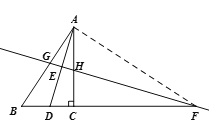
(2)∵AD平分∠BAC,∴∠BAD=∠CAD.
∵FE⊥AD,∠ACF=90°,∠AHE=∠CHF,∴∠CFH=∠CAD,∴∠BAD=∠CFH,即∠BAD=∠BFG.
(3)猜想:![]() .证明如下:
.证明如下:
连接AF.
∵EF为AD的垂直平分线,∴AF=FD,∠DAF=∠ADF,∴∠DAC+∠CAF=∠B+∠BAD.
∵AD是角平分线,∴∠BAD=∠CAD,∴∠CAF=∠ B,∴∠BAF=∠BAC+∠CAF=∠BAC+∠B=90°,∴![]() ,∴
,∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】矩形ABCO中,O(0,0),C(0,3),A(a,0),(a≥3),以A为旋转中心顺时针旋转矩形ABCO得到矩形AFED.
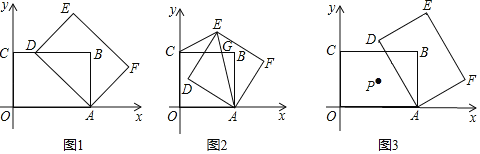
(1)如图1,当点D落在边BC上时,求BD的长(用a的式子表示);
(2)如图2,当a=3时,矩形AFED的对角线AE交矩形ABCO的边BC于点G,连结CE,若△CGE是等腰三角形,求直线BE的解析式;
(3)如图3,矩形ABCO的对称中心为点P,当P,B关于AD对称时,求出a的值,此时在x轴、y轴上是否分别存在M,N使得四边形EFMN为平行四边形,若存在直接写出M,N坐标,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动小组的同学为测量旗杆高度,先制定了如下测量方案,使用工具是测角仪和皮尺,请帮助组长林平完成方案内容,用含a,b,α的代数式表示旗杆AB的高度.
数学活动方案
活动时间:2018年4月2日 活动地点:学校操场 填表人:林平
课题 | 测量学校旗杆的高度 | ||
活动目的 | 运用所学数学知识及方法解决实际问题 | ||
方案示意图 |
| 测量步骤 | (1)用什么测得∠ADE=α; (2)用什么测得BC=a米,CD=b米. |
(3)计算过程 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
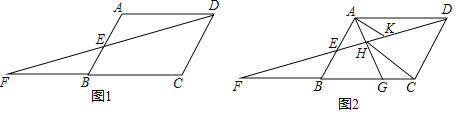
【题目】已知,如图1,在ABCD中,点E是AB中点,连接DE并延长,交CB的延长线于点F.
(1)求证:△ADE≌△BFE;
(2)如图2,点G是边BC上任意一点(点G不与点B、C重合),连接AG交DF于点H,连接HC,过点A作AK∥HC,交DF于点K.
①求证:HC=2AK;
②当点G是边BC中点时,恰有HD=nHK(n为正整数),求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
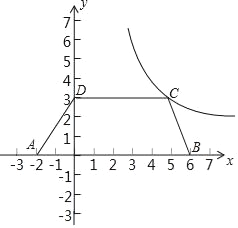
【题目】如图,在四边形ABCD中,CD∥AB,AD=BC.已知A(﹣2,0),B(6,0),D(0,3),函数y=![]() (x>0)的图象G经过点C.
(x>0)的图象G经过点C.
(1)求点C的坐标和函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)将四边形ABCD向上平移2个单位得到四边形A'B'C'D',问点B'是否落在图象G上?
查看答案和解析>>
科目:初中数学 来源: 题型:
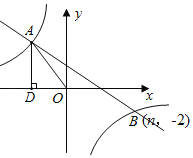
【题目】如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=
(m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=![]() ,且点B的坐标为(n,-2).
,且点B的坐标为(n,-2).
(1)求一次函数与反比例函数的解析式;
(2)E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京剧脸谱是京剧艺术独特的表现形式.京剧表演中,经常用脸谱象征人物的性格,品质,甚至角色和命运.如红脸代表忠心耿直,黑脸代表强悍勇猛.现有三张不透明的卡片,其中两张卡片的正面图案为“红脸”,另外一张卡片的正面图案为“黑脸”,卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.
请用画树状图或列表的方法,求抽出的两张卡片上的图案都是“红脸”的概率.(图案为“红脸”的两张卡片分别记为A1、A2,图案为“黑脸”的卡片记为B)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() (k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣![]() x2+4x-
x2+4x-![]() .
.
(1)用配方法把该函数解析式化为y=a(x﹣h)2+k的形式,并指出函数图象的对称轴和顶点坐标;
(2)求函数图象与x轴的交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com