
【题目】已知△ABC是等腰直角三角形,AB=![]() ,把△ABC沿直线BC向右平移得到△DEF.如果E是BC的中点,AC与DE交于P点,以直线BC为x轴,点E为原点建立直角坐标系.
,把△ABC沿直线BC向右平移得到△DEF.如果E是BC的中点,AC与DE交于P点,以直线BC为x轴,点E为原点建立直角坐标系.
(1)求△ABC与△DEF的顶点坐标;
(2)判断△PEC的形状;
(3)求△PEC的面积.
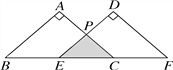
【答案】(1) A(0,1),B(-1,0),C(1,0),D(1,1),E(0,0),F(2,0);(2)△PEC是等腰直角三角形;(3)S△PEC=![]() .
.
【解析】整体分析:
(1)根据勾股定理和平移的性质求出△ABC与△DEF的顶点到点E的距离或到点A的距离;(2)根据平移的性质得DE∥AB,即可判断△PEC的形状;(3)△PEC的面积等于两条直角边乘积的一半.
解:(1)连接AE,CD.
∵△ABC是等腰直角三角形,E是BC的中点,
∴AE⊥BC,∴AE2+CE2=2CE2=AC2,∴CE=![]() AC.
AC.
∵△DEF是由△ABC平移得到的,
∴CE=AE=BE=CF=CD=![]() AC=
AC=![]() ×
×![]() =1,EF=2CE=2.
=1,EF=2CE=2.
∴A(0,1),B(-1,0),C(1,0),D(1,1),E(0,0),F(2,0).
(2)根据平移的性质,可知DE∥AB,
∴∠PEC=∠B=45°,∠EPC=∠A=90°,
∴△PEC是等腰直角三角形.
(3)S△PEC=![]() PC·PE=
PC·PE=![]() PC2=
PC2=![]() ×
×![]() CE2=
CE2=![]() .
.
所以S△PEC=![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+2的图象与反比例函数y=![]() (k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(1)求反比例函数y=![]() (k≠0)的表达式;
(k≠0)的表达式;
(2)若P是y轴上一点,且满足△ABP的面积为6,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.
(1)求证:△ABD∽△DCB;
(2)若AB=12,AD=8,CD=15,求DB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=﹣![]() x+m与y轴交于点A(0,6),直线l2:y=kx+1分别与x轴交于点B(﹣2,0),与y轴交于点C,两条直线交点记为D.
x+m与y轴交于点A(0,6),直线l2:y=kx+1分别与x轴交于点B(﹣2,0),与y轴交于点C,两条直线交点记为D.
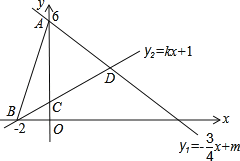
(1)m= ,k= ;
(2)求两直线交点D的坐标;
(3)根据图象直接写出y1<y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,求△BCD的周长为;
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF(要求:尺规作图,不写作法,保留作图痕迹);
②在图3中补全图形,求∠EOF的度数;
③若![]() , 求
, 求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在一条不完整的数轴上一动点A向左移动4个单位长度到达点B,再向右移动7个单位长度到达点C.
![]()
(1)若点A表示的数为0,求点B、点C表示的数;
(2)若点C表示的数为5,求点B、点A表示的数;
(3)如果点A、C表示的数互为相反数,求点B表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣22×7﹣(﹣3)×6+5;
(2)化简3(m﹣2n+2)﹣(﹣2m﹣3n)﹣1;
(3)解方程:2(2x+1)﹣(10x+1)=6;
(4)![]() =2.
=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(―1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第100次跳动至点P100的坐标是 。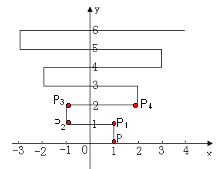
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com