
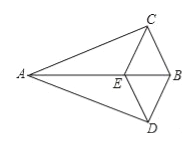
【题目】如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:
(1)∠CEB=∠CBE;
(2)四边形BCED是菱形.
科目:初中数学 来源: 题型:
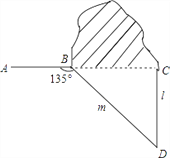
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,P为边AB上一点.
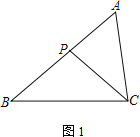
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
(2) 若M为CP的中点,AC=2,
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
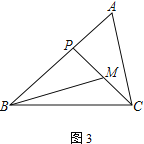
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
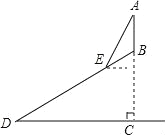
【题目】某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度,已知烈山坡面与水平面的夹角为30°,山高857.5尺,组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点,在点E处测得雕像顶端A的仰角为60°,求雕像AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰三角形,AB=AC.
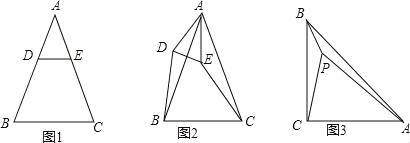
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中的任意两点![]() 我们把
我们把![]() 叫做
叫做![]() 、
、![]() 两点间的直角距离.
两点间的直角距离.
(1)已知点A(1,1),点B(3,4),则d(A,B)=________.
(2)已知点E(a,a),点F(2,2),且d(E,F)=4,则a=________.
(3)已知点M(m,2)点N(1,0),则d(M,N)的最小值为________.
(4)设![]() 是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(
是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(![]() ,Q)的最小值叫做
,Q)的最小值叫做![]() 到直线y=ax+b的直角距离,试求点M(5,1)到直线y=x+2的直角距离.
到直线y=ax+b的直角距离,试求点M(5,1)到直线y=x+2的直角距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=x2﹣2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为( )
A.y=(x﹣2)2+3
B.y=x2﹣1
C.y=(x﹣2)2+5
D.y=x2+4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com