
【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.

科目:初中数学 来源: 题型:
【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD(___ ___)
∴∠2=∠CGD(等量代换)
∴CE∥BF(__ ___)
∴∠____ ____=∠BFD(___ ____)
又∵∠B=∠C(已知)
∴____ ____(等量代换)
∴AB∥CD(___ ____)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.

(1)求证:AF=DC;
(2)若AD=CF,试判断四边形AFDC是什么样的四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
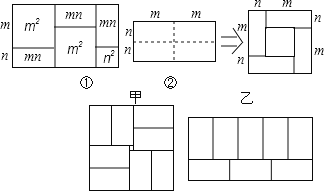
【题目】有许多代数恒等式可以用图形的面积来表示,如图①,它表示了(2m+n)(m+n)=2m2+3mn+n2.
(1)图②是将一个长2m、宽2n的长方形,沿图中虚线平方为四块小长方形,然后再拼成一个正方形,请你观察图形,写出三个代数式(m+n)2、(m-n)2、mn关系的等式: ;
(2)若已知x+y=7、xy=10,则(x-y) 2= ;
(3)小明用8个一样大的长方形(长acm,宽bcm)拼图,拼出了如图甲、乙的两种图案,图案甲是一个正方形,图案乙是一个大的长方形,图案甲的中间留下了边长是2cm的正方形小洞,则(a+2b)2-8ab的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
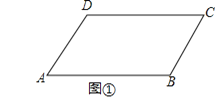
【题目】如图①,已知AD∥BC,∠B=∠D=120°.
(1)请问:AB与CD平行吗?为什么?
(2)若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.
(3)若点E在直线CD上,且满足∠EAC=![]() ∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).
∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).

查看答案和解析>>
科目:初中数学 来源: 题型:
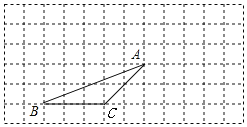
【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向上平移2格,其中每个格子的边长为1个单位长度.
(1)在图中画出平移后的△A′B′C′;
(2)若连接AA′、CC′,则这两条线段的关系是________;
(3)利用格点作直线MN,将△ABC分成面积相等的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
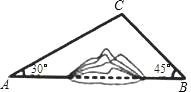
【题目】如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com