
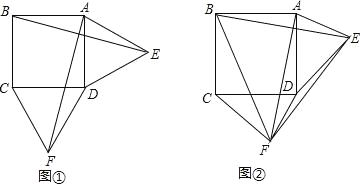
【题目】问题背景:在正方形ABCD的外侧,作△ADE和△DCF,连结AF、BE.
特例探究:如图①,若△ADE与△DCF均为等边三角形,试判断线段AF与BE的数量关系和位置关系,并说明理由;
拓展应用:如图②,在△ADE与△DCF中,AE=DF,ED=FC,且BE=4,则四边形ABFE的面积为 .
【答案】(1) 特例探究:AF=BE,AF⊥BE.理由见解析;(2)拓展应用:8.
【解析】
试题分析: 特例探究:易证△ADE≌△DCF,即可证明AF与BE的数量关系是:AF=BE,位置关系是:AF⊥BE;
拓展应用:首先证得△ADE≌△CDF,由全等三角形的性质可得∠DAE=∠CDF,易得△BAE≌△ADF,可得AE=AF,同特例探究可得AF⊥BE,易得四边形ABFE的面积为:![]() .
.
试题解析:特例探究:AF=BE,AF⊥BE.
∵四边形ABCD为正方形,△ADE与△DCF均为等边三角形,
∴AB=AD=CD,∠BAD=∠ADC,AE=AD=CD=DF,∠DAE=∠CDF,
∴∠BAD+∠DAE=∠ADC+∠CDF,即∠BAE=∠ADF,
在△ABE与△DAF中,
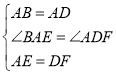 ,
,
∴△ABE≌△DAF(SAS),
∴AF=BE,∠ABE=∠DAF,
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°,
∴AF⊥BE;
拓展应用:在△ADE与△CDF中,
∵ ,
,
∴△ADE≌△CDF(SSS),
∴∠DAE=∠CDF,∠ADF=∠ADC+∠CDF=90°+∠CDF,∠BAE=∠BAD+∠EAD=90°+∠EAD,
∴∠ADF=∠BAE,
在△ABE与△DAF中,
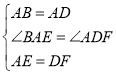 ,
,
∴△ABE≌△DAF(SAS),
∴AF=BE,∠ABE=∠DAF,
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°,
∴AF⊥BE,
∴S四边形ABFE=![]() =
=![]() ×4×4=8.
×4×4=8.


科目:初中数学 来源: 题型:
【题目】若等腰三角形中有一个角等于50°,则其它两个角的度数为( )。
A.70°
B.50°和80或65°和65°
C.65°和65°
D.50°和80°
查看答案和解析>>
科目:初中数学 来源: 题型:
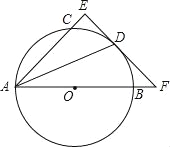
【题目】如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.
求证:EF与圆O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委为了了解学生孝敬父母的情况,在全校范围内随机抽取n名学生进行问卷调查.问卷中孝敬父母方式包括:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其他.每位学生在问卷调查时都按要求只选择了其中一种方式,该校团委收回全部问卷后,将收集到的数据整理并绘制成如下的统计图.
(1)求n的值.
(2)四种方式中被选择次数最多的方式为 (用A、B、C、D作答);选择该种方式的学生人数占被调查的学生人数的百分比为 .
(3)根据统计结果,估计该校1600名学生中选择B方式的学生比选择A方式的学生多的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个多边形的每条边都相等,每个内角都相等,且它的每一个外角与内角的度数之比为1∶2,则这个多边形是( )
A. 正五边形B. 正六边形C. 正七边形D. 正九边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 所有的有理数都有相反数
B. 正数与负数互为相反数
C. 在一个数的前面添上“-”,就得到它的相反数.
D. 在数轴上到原点距离相等的两个点所表示的数是互为相反数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com