
分析 由300、500、600的最小公倍数为3000,可设甲种零件需安排生产10x天,则乙种零件需安排生产6x天,丙种零件需安排生产5x天,根据生产的三种零件总数相等且生产三种零件的总天数为63天,即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:∵300、500、600的最小公倍数为3000,
∴3000÷300=10,3000÷500=6,3000÷600=5,
∴设甲种零件需安排生产10x天,则乙种零件需安排生产6x天,丙种零件需安排生产5x天,
根据题意得:10x+6x+5x=63,
解得:x=3,
∴10x=30,6x=18,5x=15.
答:甲种零件需安排生产30天,乙种零件需安排生产18天,丙种零件需安排生产15天.
点评 本题考查了一元一次方程的应用以及最小公倍数,找准等量关系,列出一元一次方程是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
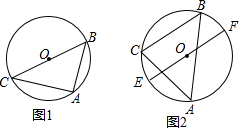 已知△ABC内接于⊙O,请仅用无刻度的直尺按要求画图:
已知△ABC内接于⊙O,请仅用无刻度的直尺按要求画图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
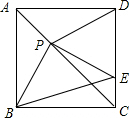 如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.
如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com