练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为（　 ）

    A. 14 B. 16 C. 17 D. 18

    【答案】D

    【解析】

    由矩形的性质得出∠ABC=90°，CD=AB=6，BC=AD=8，由勾股定理求出AC，由直角三角形斜边上的中线性质得出BP，证明PE是△ACD的中位线，由三角形中位线定理得出PE=CD=3，四边形ABPE的周长=AB+BP+PE+AE，即可得出结果．

    ∵四边形ABCD是矩形，

    ∴∠ABC=90°，CD=AB=6，BC=AD=8，

    ∴AC==10，

    ∴BP=AC=5，

    ∵P是矩形ABCD的对角线AC的中点，E是AD的中点，

    ∴AE=AD=4，PE是△ACD的中位线，

    ∴PE=CD=3，

    ∴四边形ABPE的周长=AB+BP+PE+AE=6+5+3+4=18；

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，一架长25米的梯子，斜靠在竖直的墙上，这时梯子底端离墙7米．

    （1）此时梯子顶端离地面多少米？

    （2）若梯子顶端下滑4米，那么梯子底端将向左滑动多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，二次函数的抛物线的顶点坐标C，与x轴的交于A（1，0）、B（﹣3，0）两点，与y轴交于点D（0，3）．

    （1）求这个抛物线的解析式；

    （2）如图②，过点A的直线与抛物线交于点E，交y轴于点F，其中点E的横坐标为﹣2，若直线PQ为抛物线的对称轴，点G为直线PQ上的一动点，则x轴上是否存在一点H，使D、G、H、F四点所围成的四边形周长最小？若存在，求出这个最小值及点G、H的坐标；若不存在，请说明理由；

    （3）如图③，连接AC交y轴于M，在x轴上是否存在点P，使以P、C、M为顶点的三角形与△AOM相似？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点C是线段AB上一点，分别以AC和BC为边在线段AB的同侧作等边△ACD和△BCE，连结AE和BD，相交于点F.

    （1）求证：AE=BD；

    （2）如图2.固定△BCE不动，将等边△ACD绕点C旋转（△ACD和△BCE不重叠），试问∠AFB的大小是否变化?请说明理由；

    （3）在△ACD旋转的过程中，以下结论：①CG=CH；② GF=HF； ③FC平分分∠GCH；④FC平分∠GFH；一定正确的有 （填写序号，不要求证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某计算机中有、、三个按键，以下是这三个按键的功能．

    (1)．：将荧幕显示的数变成它的正平方根，例如：荧幕显示的数为49时，按下后会变成7．

    (2)．：将荧幕显示的数变成它的倒数，例如：荧幕显示的数为25时，按下后会变成0.04．

    (3)．：将荧幕显示的数变成它的平方，例如：荧幕显示的数为6时，按下后会变成36．

    若荧幕显示的数为100时，小刘第一下按，第二下按，第三下按，之后以、、的顺序轮流按，则当他按了第100下后荧幕显示的数是多少（　　）

    A. 0.01 B. 0.1 C. 10 D. 100

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，AD∥BC，∠ABC+∠DCB＝90°，且BC＝2AD，以AB、BC、DC为边向外作正方形，其面积分别为S1、S2、S3，若S1＝4，S3＝12，则S2的值为（　　）

    A.16B.24C.48D.64

    查看答案和解析>>

    科目：初中数学 来源： 题型：

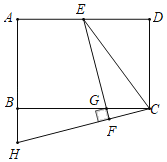
    【题目】如图，在长方形ABCD中，点E是AD的中点，连接CE，将△CDE沿着CE翻折得到△CFE，EF交BC于点G，CF的延长线交AB的延长线于点H，若AH＝25，BC＝40，则FG＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一根长为的牙刷放置在底面直径为、高为的圆柱形牙刷筒中，则牙刷露在筒外的长度最小为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC的三边长分别为3，4，5，△DEF的三边长分别为3，3x﹣2，2x+1，若这两个三角形全等，则x的值为（　　）

    A. 2 B. 2或 C. 或 D. 2或或

    查看答案和解析>>

    同步练习册答案