
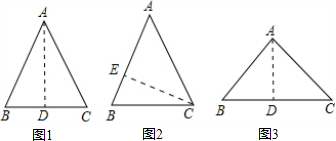
 解:(1)如图1,当底边BC=10m时,
解:(1)如图1,当底边BC=10m时,| 52+62 |
| 61 |
| 61 |
| 10 |
| 10 |
| 1 |
| 2 |
|
|
|
| 10 |
| 10 |
| 61 |
| 10 |
| 10 |


科目:初中数学 来源: 题型:
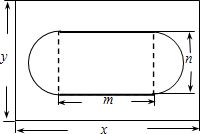 某居民小区为了美化环境,要在一块长为x,宽为y的矩形绿地上建造花坛,要求花坛所占面积不超过绿地面积的一半,小明为此设计一个如图的方案,花坛是由一个矩形和两个半圆组成的,其中m,n分别是x,y的
某居民小区为了美化环境,要在一块长为x,宽为y的矩形绿地上建造花坛,要求花坛所占面积不超过绿地面积的一半,小明为此设计一个如图的方案,花坛是由一个矩形和两个半圆组成的,其中m,n分别是x,y的| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2012年黑龙江省齐齐哈尔市某校中考数学模拟试卷(二)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:江苏省期中题 题型:解答题
 ,若x=
,若x= y,则小明的设计方案是否符合要求?请你用方法加以说明。
y,则小明的设计方案是否符合要求?请你用方法加以说明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com