
【题目】如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9. 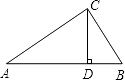
(1)求DC的长.
(2)求AB的长.
【答案】
(1)解:∵CD⊥AB于D,且BC=15,BD=9,AC=20
∴∠CDA=∠CDB=90°
在Rt△CDB中,CD2+BD2=CB2,
∴CD2+92=152
∴CD=12
(2)解:在Rt△CDA中,CD2+AD2=AC2
∴122+AD2=202
∴AD=16,
∴AB=AD+BD=16+9=25
【解析】(1)由题意可知三角形CDB是直角三角形,利用已知数据和勾股定理直接可求出DC的长;(2)有(1)的数据和勾股定理求出AD的长,进而求出AB的长.
【考点精析】掌握勾股定理的概念是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】某同学抽取一个学习小组统计这些同学本学期的用笔情况,结果如下表:
用笔数(支) | 4 | 5 | 6 | 8 | 9 |
学生数 | 4 | 4 | 7 | 3 | 2 |
则关于这20名学生本学期的用笔数量,下列说法错误的是( ) .
A. 中位数是6支 B. 平均数是6支 C. 众数是6支 D. 方差是5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设正方体ABCD﹣A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是( ) 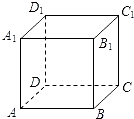
A.0
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂工业废气年排放量为400万立方米,为改善大气环境质量,决定分二期投入治理,使废气的年排放量减少到256万立方米,如果每期治理中废气减少的百分率相同.求每期减少的百分率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)当m取满足条件的最小整数时,求方程的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com