分析:(1)点P在AD段的运动时间为2s,则DP的长度为(t-2)cm;
(2)当点N落在AB边上时,有两种情况,如图(2)所示.利用运动线段之间的数量关系求出时间t的值;
(3)当正方形PQMN与△ABC重叠部分图形为五边形时,有两种情况,分别用时间t表示各相关运动线段的长度,如图(3)a利用“S=S
梯形AQPD-S
△AMF=
(PD+AQ)•PQ-
AM•FM”求出面积S的表达式;如图(3)b利用“S=S
梯形AQPG-S
△AMF=
(PG+AC)•PC-
AM•FM”求出面积S的表达式;
(4)本问涉及双点的运动,首先需要正确理解题意,然后弄清点H、点P的运动过程:
当4<t<6时,此时点P在线段DE上运动,如图(4)a所示.此时点H将两次落在线段CD上;
当6≤t≤8时,此时点P在线段EB上运动,如图(4)b所示.此时MN与CD的交点始终是线段MN的中点,即点H.
解答:解:(1)∵在Rt△ABC中,AC=8cm,BC=4cm,
∴AB=
=
=
4,
D为AB中点,∴AD=
2,
∴点P在AD段的运动时间为
=2s.
当点P在线段DE上运动时,DP段的运动时间为(t-2)s,
∵DE段运动速度为1cm/s,∴DP=(t-2)cm.
(2)当点N落在AB边上时,有两种情况,如下图所示:

①如图(2)a,此时点D与点N重合,P位于线段DE上.
由三角形中位线定理可知,DM=
BC=2,∴DP=DM=2.
由(1)知,DP=t-2,∴t-2=2,∴t=4;
②如图(2)b,此时点P位于线段EB上.
∵DE=
AC=4,∴点P在DE段的运动时间为4s,
∴PE=t-6,∴PB=BE-PE=8-t,PC=PE+CE=t-4.
∵PN∥AC,∴PN:PB=AC:BC=2,∴PN=2PB=16-2t.
由PN=PC,得16-2t=t-4,解得t=
.
所以,当点N落在AB边上时,t=4或t=
.
(3)当正方形PQMN与△ABC重叠部分图形为五边形时,有两种情况,如下图所示:

①当2<t<4时,如图(3)a所示.
DP=t-2,PQ=2,∴CQ=PE=DE-DP=4-(t-2)=6-t,AQ=AC-CQ=2+t,AM=AQ-MQ=t.
∵MN∥BC,∴FM:AM=BC:AC=1:2,∴FM=
AM=
t.
S=S
梯形AQPD-S
△AMF=
(DP+AQ)•PQ-
AM•FM=
[(t-2)+(2+t)]×2-
t•
t=-
t
2+2t;
②当
<t<8时,如图(3)b所示.
PE=t-6,∴PC=CM=PE+CE=t-4,AM=AC-CM=12-t,PB=BE-PE=8-t,
∴FM=
AM=6-
t,PG=2PB=16-2t,
S=S
梯形AQPG-S
△AMF=
(PG+AC)•PC-
AM•FM=
[(16-2t)+8]×(t-4)-
(12-t)•(6-
t)=
-t
2+22t-84.
综上所述,S与t的关系式为:S=
| | -t2+2t(2<t<4) | | -t2+22t-84(<t<8) |
| |
(4)依题意,点H与点P的运动分为两个阶段,如下图所示:
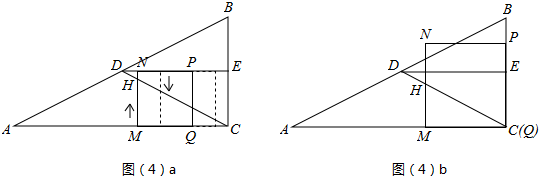
①当4<t≤6时,此时点P在线段DE上运动,如图(4)a所示.
此阶段点P运动时间为2s,因此点H运动距离为2.5×2=5cm,而MN=2,
则此阶段中,点H将有3次机会落在线段CD上:
第一次:此时点H由M→H运动时间为(t-4)s,运动距离MH=2.5(t-4)cm,∴NH=2-MH=12-2.5t;
又DP=t-2,DN=DP-2=t-4,由DN=2NH得到:t-4=2(12-2.5t),解得t=
;
第二次:此时点H由N→H运动时间为t-4-
=(t-4.8)s,运动距离NH=2.5(t-4.8)=2.5t-12;
又DP=t-2,DN=DP-2=t-4,由DN=2NH得到:t-4=2(2.5t-12),解得t=5;
②当6≤t≤8时,此时点P在线段EB上运动,如图(4)b所示.
由图可知,在此阶段,始终有MH=
MC,即MN与CD的交点始终为线段MN的中点,即点H.
综上所述,在点P的整个运动过程中,点H落在线段CD上时t的取值范围是:t=
或t=5或6≤t≤8.

 线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在线段AQ上.设点P的运动时间为t(s).
线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在线段AQ上.设点P的运动时间为t(s).

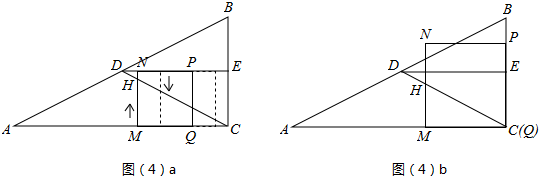


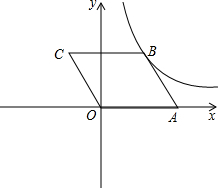 (2012•长春)如图,在平面直角坐标系中,?OABC的顶点A、C的坐标分别为A(2,0)、C(-1,2),反比例函数y=
(2012•长春)如图,在平面直角坐标系中,?OABC的顶点A、C的坐标分别为A(2,0)、C(-1,2),反比例函数y=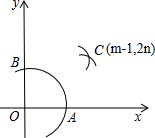 (2012•长春)如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于
(2012•长春)如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于 (2012•长春)如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.这组数据的中位数是( )
(2012•长春)如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.这组数据的中位数是( )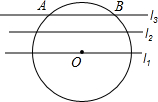 (2012•长春)如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.
(2012•长春)如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.