
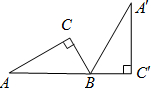
 如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,求斜边AB旋转到A′B所扫过的扇形面积.
如图,Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C′在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,求斜边AB旋转到A′B所扫过的扇形面积.| nπr2 |
| 360 |
| nπr2 |
| 360 |
| 120π×16 |
| 360 |
| 16π |
| 3 |
| 16π |
| 3 |
| nπr2 |
| 360 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
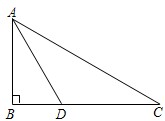 如图,某中学九年级数学兴趣小组测量校内旗杆AB高度,在C点测得旗杆顶端A的仰角为30°,向前走了26米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度忽略不计,点B、D、C在同一直线上),求旗杆AB的高度(结果保留3个有效数字,
如图,某中学九年级数学兴趣小组测量校内旗杆AB高度,在C点测得旗杆顶端A的仰角为30°,向前走了26米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度忽略不计,点B、D、C在同一直线上),求旗杆AB的高度(结果保留3个有效数字,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、3.3×109元 |
| B、3.3×1010元 |
| C、3.3×1011元 |
| D、3.3×1012元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
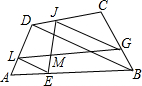 如图,在四边形ABCD的各边上取点E、G,J,L,已知
如图,在四边形ABCD的各边上取点E、G,J,L,已知| AE |
| AB |
| DJ |
| DC |
| 1 |
| 3 |
| AL |
| AD |
| BG |
| BC |
| 1 |
| 3 |
| LM |
| LG |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 10 |
| x |
| b |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com