
【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕着矩形ABCD(AB<BC)的对角线交点O旋转(如图①→②→③),图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点.
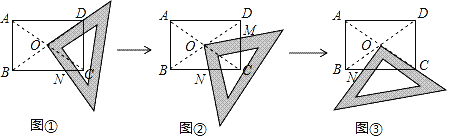
(1)该学习小组中一名成员意外地发现:在图①(三角板的一直角边与OD重合)中,BN2=CD2+CN2;在图③(三角板的一直角边与OC重合)中,CN2=BN2+CD2.请你对这名成员在图①和图③中发现的结论选择其一说明理由.
(2)试探究图②中BN、CN、CM、DM这四条线段之间的关系,写出你的结论,并说明理由.
【答案】(1)见解析;(2)见解析.
【解析】
(1)连接DN,根据矩形得出OB=OD,根据线段垂直平分线得出BN=DN,根据勾股定理求出DN的平方,即可求出答案;
(2)延长NO交AD于点P,连接PM,MN,证△BNO≌△DPO,推出OP=ON,DP=BN,根据线段垂直平分线求出PM=MN,根据勾股定理求出即可.
(1)选①.证明如下:连接DN,
∵四边形ABCD是矩形,∴OB=OD,
∵∠DON=90°,∴BN=DN,
∵∠BCD=90°,∴DN2=CD2+CN2,∴BN2=CD2+CN2;
(2)延长NO交AD于点P,连接PM,MN,
∵四边形ABCD是矩形,∴OD=OB,AD∥BC,∴∠DPO=∠BNO,∠PDO=∠NBO,
在△BON和△DOP中,∵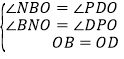 ,∴△BON≌△DOP(AAS),∴ON=OP,BN=PD,
,∴△BON≌△DOP(AAS),∴ON=OP,BN=PD,
∵∠MON=90°,∴PM=MN,
∵∠ADC=∠BCD=90°,∴PM2=PD2+DM2,MN2=CM2+CN2,∴PD2+DM2=CM2+CN2,∴BN2+DM2=CM2+CN2.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.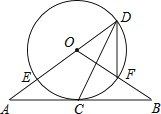
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生的交通安全意识,某中学和交警大队联合举行了“我当一日小交警”活动,星期天选派部分学生到交通路口值勤,协助交通警察维护交通秩序.若每一个路口安排4人,那么还剩下78人;若每个路口安排8人,那么最后一个路口不足8人,但不少于4人.求这个中学共选派值勤学生多少人?共有多少个交通路口安排值勤?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,航空母舰始终以40千米/时的速度由西向东航行,飞机以800千米/时的速度从舰上起飞,向西航行执行任务,如果飞机在空中最多能连续飞行4个小时,那么它在起飞_____小时后就必须返航,才能安全停在舰上?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )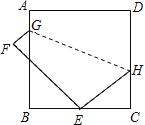
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习一次函数的经验,对函数y=|2x﹣1|的图象和性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=|2x﹣1|的自变量x的取值范围是 ;
(2)已知:
①当x=![]() 时,y=|2x﹣1|=0;
时,y=|2x﹣1|=0;
②当x>![]() 时,y=|2x﹣1|=2x﹣1
时,y=|2x﹣1|=2x﹣1
③当x<![]() 时,y=|2x﹣1|=1﹣2x;
时,y=|2x﹣1|=1﹣2x;
显然,②和③均为某个一次函数的一部分.
(3)由(2)的分析,取5个点可画出此函数的图象,请你帮小东确定下表中第5个点的坐标(m,n),其中m= ;n= ;:
x | … | ﹣2 | 0 |
| 1 | m | … |
y | … | 5 | 1 | 0 | 1 | n | … |
(4)在平面直角坐标系xOy中,作出函数y=|2x﹣1|的图象;
(5)根据函数的图象,写出函数y=|2x﹣1|的一条性质.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是工人师傅用同一种材料制成的金属框架,已知![]() ,
,![]() ,
,![]() ,其中
,其中![]() 的周长为24cm,
的周长为24cm,![]() ,则制成整个金属框架所需这种材料的总长度为( )
,则制成整个金属框架所需这种材料的总长度为( )

A. 45cm B. 48cm C. 51cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
①0是绝对值最小的有理数;②相反数大于本身的数是负数;③数轴上原点两侧的数互为相反数;![]() 是有理数.
是有理数.
A. ①② B. ①③ C. ①②③ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com