练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．如果关于x的不等式$\frac{3x-a}{5}＜\frac{1-x}{2}$的解集为x＜2，求a的值．

    分析 解不等式求得x＜$\frac{5+2a}{11}$，由解集为x＜2得$\frac{5+2a}{11}$=2，解之即可得．

    解答 解：去分母，得：2（3x-a）＜5（1-x），
    去括号，得：6x-2a＜5-5x，
    移项，得：6x+5x＜5+2a，
    合并同类项，得：11x＜5+2a，
    系数化为1，得：x＜$\frac{5+2a}{11}$，
    由题意知$\frac{5+2a}{11}$=2，
    解得：a=$\frac{17}{2}$．

    点评 本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

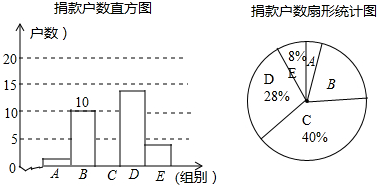    8．某社区居民参加献爱心活动，为了解该社区居民捐款情况，对社区部分捐款户数进行分组统计，数据整理成如图所示的不完整统计图．已知A、B两组捐款户数直方图的高度比为1：5，请结合图中相关数据回答下列问题．
    捐款分组统计表：
    组别捐款额（x）元
    A10≤x＜100
    B　100≤x＜200
    C　200≤x＜300
    D　300≤x＜400
    E　x≥400
    （1）求本次调查样本的容量和扇形统计图中A组对应扇形的圆心角度数．
    （2）求出C组的频数，并补全直方图．
    （3）若该社区有600户住户，请估计捐款不少于300元的户数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．几何计算

    （1）如图1，∠AOC，∠BOD都是直角，且∠AOB与∠AOD的度数比是2：11，求∠BOC的度数．
    （2）如图2，点C分线段AB为5：7，AC＜BC，点D分线段AB为5：11，若CD=10cm，求AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．一个多边形的内角和与它的外角和的比为5：2，则这个多边形的边数为（　　）
    A．8B．7C．6D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．若$\sqrt{3x+1}$在实数范围内有意义，则x的取值范围是（　　）
    A．x$＞\frac{1}{3}$B．x≥$\frac{1}{3}$C．x≥-$\frac{1}{3}$D．x＞-$\frac{1}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知a：b=3：4，b：c=3：5，求a：b：c．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．扇形的半径为3cm，圆心角为120°，用它做一个圆锥模型的侧面，这个圆锥的高为2$\sqrt{2}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，抛物线y=-$\frac{\sqrt{3}}{3}$x2-$\sqrt{3}$x+$\frac{4\sqrt{3}}{3}$与x轴交于A，B两点（A点在B点的左侧），与y轴交于点C，已知点D（0，-$\sqrt{3}$）．
    （1）求直线AC的解析式；
    （2）如图1，P为直线AC上方抛物线上的一动点，当△PBD面积最大时，过P作PQ⊥x轴于点Q，M为抛物线对称轴上的一动点，过M作y轴的垂线，垂足为点N，连接PM，NQ，求PM+MN+NQ的最小值；
    （3）在（2）问的条件下，将得到的△PBQ沿PB翻折得到△PBQ′，将△BPQ′沿直线BD平移，记平移中的△PBQ′为△P′B′Q″，在平移过程中，设直线P′B′与x轴交于点E．则是否存在这样的点E，使得△B′EQ″为等腰三角形？若存在，求此时OE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

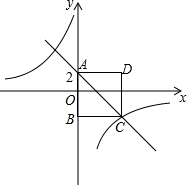    10．如图，四边形ABCD为正方形．点A的坐标为（0，2），点B的坐标为（0，-3）．反比例函数y=$\frac{k}{x}$图象经过点C，一次函数y=ax+b的图象经过点A、C．
    （1）求反比例函数与一次函数的解析式；
    （2）观察图象，直接写出在第四项限内使得$\frac{k}{x}$＜ax+b成立的自变量x的取值范围；
    （3）若点P是反比例函数图象上的一点，且△OAP的面积恰好等于正方形ABCD的面积，求P点的坐标．

    查看答案和解析>>

    同步练习册答案