
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)求证:四边形DEFG是平行四边形.
(2)若AB=AC,则四边形DEFG是 (填写特殊的平行四边形).
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.

【答案】(1)见解析;(2)矩形;(3)4![]() +4.
+4.
【解析】
(1)利用DE为△ABC的中位线得到DE∥BC,DE=![]() BC,利用FG为△OBC的中位线得到FG∥BC,FG=
BC,利用FG为△OBC的中位线得到FG∥BC,FG=![]() BC,则ED=FG,ED∥FG,然后根据平行四边形的判定方法得到结论;
BC,则ED=FG,ED∥FG,然后根据平行四边形的判定方法得到结论;
(2)利用等腰三角形腰上的中线相等得到BD=CE,再根据三角形重心性质得到OD=![]() BD,OE=
BD,OE=![]() CE,所以OD=OE,然后根据矩形的判定方法得到四边形DEFG是矩形;
CE,所以OD=OE,然后根据矩形的判定方法得到四边形DEFG是矩形;
(3)利用正方形的性质得到OE=OD=![]() DE=
DE=![]() ,∠DOE=90°,则OB=OC=2OD=2
,∠DOE=90°,则OB=OC=2OD=2![]() ,再利用勾股定理计算出BE=CD=
,再利用勾股定理计算出BE=CD=![]() ,所以AB=AC=2
,所以AB=AC=2![]() ,由于BC=2DE=4,然后计算△ABC的周长.
,由于BC=2DE=4,然后计算△ABC的周长.
(1)证明:∵BD和CE为△ABC的中线,
∴DE为△ABC的中位线,
∴DE∥BC,DE=![]() BC,
BC,
∵F,G分别是BO,CO的中点,
∴FG为△OBC的中位线,
∴FG∥BC,FG=![]() BC,
BC,
∴ED=FG,ED∥FG,
∴四边形DEFG是平行四边形;
(2)解:∵AB=AC,
∴BD=CE,
∵点O为△ABC的重心,
∴OD=![]() BD,OE=
BD,OE=![]() CE,
CE,
∴OD=OE,
∵四边形DEFG为平行四边形,
∴四边形DEFG是矩形;
故答案为:矩形;
(3)解:∵四边形DEFG是正方形,
∴OE=OD=![]() DE=
DE=![]() ,∠DOE=90°,
,∠DOE=90°,
∴OB=OC=2OD=2![]() ,
,
在Rt△BOE中,BE=![]() ,
,
同理得CD=![]() ,
,
∴AB=AC=2![]() ,
,
∵BC=2DE=4,
∴△ABC的周长=2![]() +2
+2![]() +4=4
+4=4![]() +4.
+4.


科目:初中数学 来源: 题型:
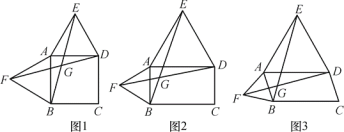
【题目】以四边形ABCD的边AB,AD为边分别向外侧作等边△ABF和等边△ADE,连接EB,FD,交点为G.
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一根长22cm的铁丝:
(1)能否围成面积是30cm2的扇形?若能,求出扇形半径;若不能,请说明理由.
(2)能否围成面积是32cm2的扇形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、CD于M、N两点.若AM=4,则BM=_____,ON=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y﹣2与x成正比例,当x=2时,y=6.
(1)求y与x之间的函数解析式.
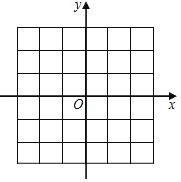
(2)在所给直角坐标系中画出函数图象.
(3)此函数图象与x轴交于点A,与y轴交于点B,点C在x轴上,若S△ABC=3,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
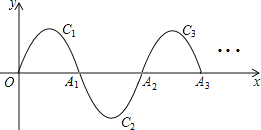
【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C17.
(1)写出点![]() 的坐标________
的坐标________
(2)若P(50,m)在第17段抛物线C17上,则m=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
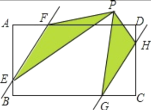
【题目】如图,在矩形ABCD中,AD=6,AB=5,点E、F、G、H分别在AD、AB、BC、CD上,且AF=CG=1,BE=DH=2,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,设甲、乙、丙、丁分别表示△ABC,△ACD,△EFG,△EGH.已知∠ACB=∠CAD=∠EFG=∠EGH=70°,∠BAC=∠ACD=∠EGF=∠EHG=50°,则叙述正确的是( )
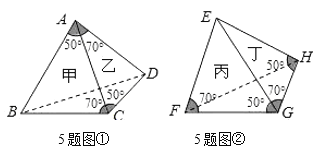
A.甲、乙全等,丙、丁全等B.甲、乙全等,丙、丁不全等
C.甲、乙不全等,丙、丁全等D.甲、乙不全等,丙、丁不全等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com