
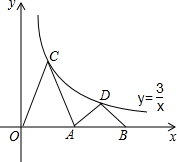
 如图,点C、D在双曲线y=$\frac{3}{x}$(x>0)上,点A、B在x轴上,且OA=AB,CO=CA,DA=DB,则S△OCA+S△ADB=4.
如图,点C、D在双曲线y=$\frac{3}{x}$(x>0)上,点A、B在x轴上,且OA=AB,CO=CA,DA=DB,则S△OCA+S△ADB=4. 分析 作CM⊥x轴于M,DN⊥x轴于N,连结OD,根据等腰三角形的性质得OM=AM=$\frac{1}{2}$OA,AN=BN=$\frac{1}{2}$AB,则利用三角形面积公式得到S△MOC=S△MAC,S△NAD=S△NBD,再利用反比例函数的比例系数k的几何意义得S△MOC=S△NOD=$\frac{1}{2}$×3=1.5,又OA=AB,根据三角形面积公式得到S△NAD=$\frac{1}{2}$S△OAD=$\frac{1}{3}$S△NOD=0.5,所以S△OCA+S△ADB=4.
解答 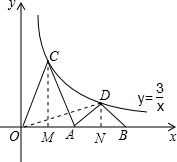 解:作CM⊥x轴于M,DN⊥x轴于N,连结OD,如图,
解:作CM⊥x轴于M,DN⊥x轴于N,连结OD,如图,
∵CO=CA,DA=DB,
∴OM=AM=$\frac{1}{2}$OA,AN=BN=$\frac{1}{2}$AB,
∴S△MOC=S△MAC,S△NAD=S△NBD.
∵点C、D在双曲线y=$\frac{3}{x}$(x>0)上,
∴S△MOC=S△NOD=$\frac{1}{2}$×3=1.5,
又∵OA=AB,
∴S△NAD=$\frac{1}{2}$S△OAD=$\frac{1}{3}$S△NOD=0.5,
∴S△OCA+S△ADB=2S△MOC+2S△NAD=2×1.5+2×0.5=4.
故答案为4.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了等腰三角形的性质.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
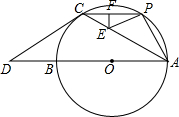 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,已知CD=CA.
如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,已知CD=CA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
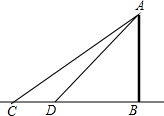 如图所示,对岸有一铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进16米到达D,在D处测得A的仰角为40°,求铁塔AB的高.(结果保留整数)
如图所示,对岸有一铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进16米到达D,在D处测得A的仰角为40°,求铁塔AB的高.(结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
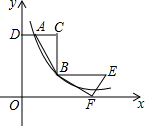 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,延长CA交y轴于点D,AD=1.
如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,延长CA交y轴于点D,AD=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com