
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤ ![]() ,其中正确结论有( )个
,其中正确结论有( )个
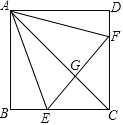
A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】∵四边形ABCD是正方形,△AEF是等边三角形,
∴AB=BC=CD=AD,AE=AF=EF,∠B=∠D=∠BCD=90°,∠EAF=60°,
∴△ABE≌△ADF,∠BAE+∠DAF=90°-60°=30°,
∴∠BAE=∠DAF=15°,BE=DF,(即①②正确);
∴BC-BE=DC-DF,即CE=CF,
又∵AE=AF,
∴点A、C都在线段EF的垂直平分线上,
∴AC垂直平分EF.(即③正确);
如下图,在AB上取点P连接PE,使PE=PA,则由∠BAE=15°可知∠BPE=30°,
设BE=DF=1,则PE=PA=2,在Rt△PEB中由勾股定理可得:PB=![]() ,
,
∴AB=BC=DC=![]() ,
,
∴CE=CF=BC-BE=![]() ,
,
∴EF=![]() EC=
EC=![]() ,
,
∵BE+DF=2,
∴BE+DF![]() EF.(即④错误);
EF.(即④错误);
∵S△CEF=![]() CE2=
CE2=![]() ,2S△ABE=
,2S△ABE=![]() AB·BE=
AB·BE=![]() ,
,
∴S△CEF=2S△ABE(即⑤正确);
综上所述,上述5个结论中,正确的有4个.
故选C.



 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,DF恰好分别经过点B、C.
(1)∠DBC+∠DCB= 度;
(2)过点A作直线直线MN∥DE,若∠ACD=20°,试求∠CAM的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今很多初中生购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:
A:自带白开水;B:瓶装矿泉水;C:碳酸饮料;D:非碳酸饮料.
根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题:
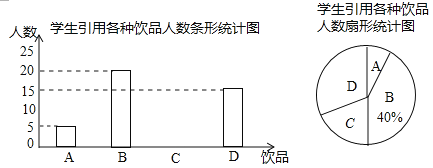
(1)这个班级有多少名同学?并补全条形统计图.
(2)若该班同学没人每天只饮用一种饮品(每种仅限1瓶,价格如下表),则该班同学用于饮品上的人均花费是多少元?

(3)若我市约有初中生4万人,估计我市初中生每天用于饮品上的花费是多少元?
(4)为了养成良好的生活习惯,班主任决定在自带白开水的5名同学(男生2人,女生3人)中随机抽取2名同学做良好习惯监督员,请用列表法或树状图法求出恰好抽到2名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在体育课上,对七年级男生进行引体向上测试.以做4个为标准,超过的个数记作正数,不足的个数记作负数其中8名男生做引体向上的个数记录如下:
+3 | -1 | 1 | +3 | 1 | 0 | +2 | -1 |
这8名男生平均每人做了多少个引体向上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC∽△A`B`C`, ![]() ,边上的中线CD=4cm,△ABC的周长为20cm,△A`B`C`的面积是64 cm2,求:
,边上的中线CD=4cm,△ABC的周长为20cm,△A`B`C`的面积是64 cm2,求:
(1)A`B`边上的中线C`D`的长;
(2)△A`B`C`的周长
(3)△ABC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直X轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com