Question

4．如图，已知直线l₁∥l₂，一个45°角的顶点A在l₁上，过A作AD⊥l₂，垂足为D，AD=6．将这个角绕顶点A旋转（角的两边足够长）．
（1）如图，旋转过程中，若角的两边与l₂分别交于B、C，且AB=AC，求BD的长．为了解决这个问题，下面提供一种解题思路：如图，作∠DAP=45°，AP与l₂相交于点P，过点C作CQ⊥AP于点Q．∵∠DAP=∠BAC=45°，∴∠BAD=∠CAQ，请你接下去完成解答．
（2）旋转过程中，若角的两边与l₂分别交于E、F（E在F左面），且AE＞AF，DF=2，求DE的长．请你借鉴（1）的做法在备用图中画图并解答这个问题．

Answer 1

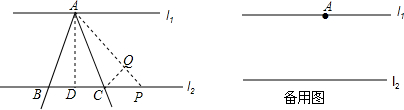
分析 （1）先根据全等三角形的判定和性质得出BD=CQ，AQ=AD，再得出△ADP、△CQP是等腰直角三角形，进而得出答案即可；
（2）分E，F分别位于AD的同侧和两侧这两种情况进行分析，再根据相似三角形的性质和等腰直角三角形的性质进行解答即可．

解答 解：（1）∵AD⊥l₂，CQ⊥AP，
∴∠ADB=∠AQC=90°，
又∵AB=AC，
在△ABD和△ACQ中，
$\left\{\begin{array}{l}{∠BAD=∠CAQ}\\{∠ADB=∠AQC}\\{AB=AC}\end{array}\right.$，
∴△ABD≌△ACQ（AAS），
∴BD=CQ，AQ=AD=6，
∵∠DAP=∠BAC=45°，
∴△ADP、△CQP是等腰直角三角形，
∴AP=$6\sqrt{2}$，
∴QP=$6\sqrt{2}-6$，
∴BD=CQ=QP=$6\sqrt{2}-6$．
（2）①如图1：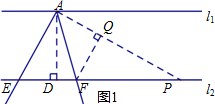
作∠DAP=45°，AP与l₂相交于点P，过点F作FQ⊥AP于点Q．
∵∠DAP=∠EAF=45°，
∴∠EAD=∠FAQ，
∵AD⊥l₂，FQ⊥AP，
∴∠ADE=∠AQF=90°，
∴△AED∽△AFQ，
∴$\frac{DE}{FQ}=\frac{AD}{AQ}$．
∴△ADP、△FQP是等腰直角三角形，
∴DP=AD=6，AP=$6\sqrt{2}$，
∵DF=2，
∴FP=DP-DF=4，
∴FQ=QP=$2\sqrt{2}$，
∴AQ=$6\sqrt{2}-2\sqrt{2}=4\sqrt{2}$，
∴$\frac{DE}{2\sqrt{2}}=\frac{6}{4\sqrt{2}}$，
∴DE=3．  
②如图2：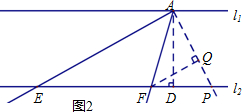
作∠DAP=45°，AP与l₂相交于点P，过点F作FQ⊥AP于点Q．
∵∠DAP=∠EAF=45°，
∴∠EAD=∠FAQ，
∵AD⊥l₂，FQ⊥AP，
∴∠ADE=∠AQF=90°，
∴△AED∽△AFQ，
∴$\frac{DE}{FQ}=\frac{AD}{AQ}$  
∴△ADP、△FQP是等腰直角三角形，
∴DP=AD=6，AP=6$\sqrt{2}$，
∵DF=2，
∴FP=DP+DF=8，
∴FQ=QP=4$\sqrt{2}$，
∴AQ=$6\sqrt{2}-4\sqrt{2}=2\sqrt{2}$，
∴$\frac{DE}{4\sqrt{2}}=\frac{6}{2\sqrt{2}}$，
∴DE=12．

点评 此题考查几何变换问题，关键是根据全等三角形和相似三角形的判定和性质分析，同时利用等腰直角三角形的性质对边的长度进行计算得出答案．