
��ͼ��ʾ�������壬�������չ��������������ͼ���е�( )

A.  B.
B.  C.
C. 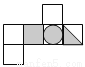 D.
D. 

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰��ϲ��23�� ��ת ��Ԫ���Ծ� ���ͣ������
��ͼ���ı���ABCD�DZ߳�Ϊ2��һ����ǵ���60�������ֽƬ��С��ͬѧ��һ��������ֽƬ��һ������������ζ���D�غϣ���˳ʱ�뷽����ת������ֽƬ��ʹ�������߷ֱ�CB��BA�������ǵ��ӳ��ߣ��ڵ�E��F����EDF=60�㣬��CE=AFʱ����ͼ1С��ͬѧ�ó��Ľ�����DE=DF��

��1��������ת������ֽƬ����CE��AFʱ����ͼ2С���Ľ����Ƿ������������������֤����������������˵�����ɣ�
��2���ٴ���ת������ֽƬ������E��F�ֱ���CB��BA���ӳ�����ʱ����ͼ3��ֱ��д��DE��DF��������ϵ��
��3����EF������DEF�����Ϊy��CE=x����y��x�Ĺ�ϵʽ����ָ����xΪ��ֵʱ��y����Сֵ����Сֵ�Ƕ��٣�
(1)������֤������������2��DF=DE����3����x=0ʱ��y��Сֵ=�� �������� �����������1����ͼ1������BD�����������������֤����ADF=��BDE��Ȼ��֤����ADF�ա�BDE��ASA������DF=DE�� ��2����ͼ2������BD�����������������֤����ADF=��BDE��Ȼ��֤����ADF�ա�BDE��ASA������DF=DE�� ��3�����ݣ�2���еġ�ADF�ա�BDE�õ���S...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰��ϲ��25�� ���ʳ��� ��Ԫ���Ծ� ���ͣ���ѡ��
��������10����������ɸ�������Щ�����ɫ���������ͬ��С���Ӵ������зŻص�����������100�Σ������������������25�Σ�������������Լ�У� ��
A. 20�� B. 30�� C. 40�� D. 50��
B ��������������������Լ��x������������ɵã� �����x=30����ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶��ѧ���п���ģ��ѧ�Ծ� ���ͣ������
����ijʮ��·�ڵ������������ܼ���ֱ�У�Ҳ��������ת������ת����������ֿ����Դ�С��ͬ�����������������ʮ��·�ڣ����Ƕ�����ֱ�еĸ�����_________.
������������������б��ã� ���ܳ��ֵĽ����9�֣����dz��ֵĿ�������ͬ�� P��������ȫ������ֱ�У�=. �ʴ�Ϊ�� .�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶��ѧ���п���ģ��ѧ�Ծ� ���ͣ���ѡ��
��ͼ��ʾ��һ��ͶӰ�����뽺Ƭ��ͼ���Ͷ����Ļ��. ��֪��Ƭ����Ļƽ�У�A��Ϊ��Դ���뽺ƬBC�ľ���Ϊ0.1�ף���Ƭ�ĸ�BCΪ0.038�ף�����ҪͶӰ���ͼ��DE��1.9�ף���ͶӰ����Դ����Ļ��ԼΪ( )
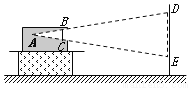
A. 6�� B. 5�� C. 4�� D. 3��
B �������������������ͼ��ʾ����A��AG��DE��G����BC��F ��ΪBC��DE�����ԡ�ABC�ס�ADE��AG��BC��AF=0.1m����AG=h�� �� ��������ã�h=5m�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ���ڶ�ʮ���� ������ ���ͣ������
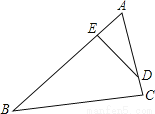
��ͼ����֪��ABC�ס�ADE��AB=30cm��AD=18cm��BC=20cm����BAC=75�㣬��ABC=40�㣮
��1�����ADE�͡�AED�Ķ�����
��2����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ���ڶ�ʮ���� ������ ���ͣ������
��ͼ���ڡ�ABC�У�AB��9��AC��6��BC��12����M�ڱ�AB�ϣ�AM��3������M��ֱ��MN���AC���ڵ�N��ʹ�صõ���������ԭ������ABC���ƣ���MN�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����ʡ��������������������꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ������
�̳�����һ��������ÿ����۳�20����ÿ��ӯ��40Ԫ��Ϊ���������ۼ��ٿ�棬������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣����һ������ÿ����1Ԫ��ÿ��ɶ��۳�2����
����ÿ������xԪ��ÿ��ӯ��yԪ���г�y��x֮��ĺ�����ϵʽ��
�����̳�ÿ��Ҫӯ��1200Ԫ��ÿ���������۶���Ԫ��
��ÿ�����۶���Ԫʱ���̳�ÿ���ӯ���ﵽ���ӯ������Ƕ���Ԫ��
��y=��2x2+60x+800�����̳�ÿ��Ҫӯ��1200Ԫ��ÿ����������20Ԫ����ÿ������15Ԫʱ���̳�ÿ���ӯ���ﵽ���ӯ�������1250Ԫ�� �������� ����������ٸ���ÿ��ӯ������ÿ����������ۼ����õ�y=��40��x����20+2x�����������ɣ� ����y=1200���õ���2x2+60x+800=1200��������x2��30x+20=0��Ȼ��������ʽ�ֽⷨ�⼴�ɣ� �۰�y=...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݽ���2016-2017ѧ�����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ���ѡ��
��ͼ����һ�����ǰ������һ��ʹֱ�ǵĶ����غ��� ����
����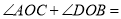 �� ����
�� ����

A.  B.
B.  C.
C.  D.
D. 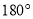
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com