
【题目】(问题背景)在面积都相等的所有矩形中,当其中一个矩形的一边长为![]() 时,它的另一边长为
时,它的另一边长为![]() .求周长
.求周长![]() 的取值范围.
的取值范围.
(建立模型)
(1)设矩形相邻两边的长分别为![]() ,
,![]() ,由题意可得
,由题意可得![]() ,则
,则![]() ,由周长为
,由周长为![]() ,得
,得![]() ,即
,即![]() ,满足要求的
,满足要求的![]() 的取值,从“图形”角度考虑,应是函数
的取值,从“图形”角度考虑,应是函数![]() 与 的图象在第一象限内有公共点时
与 的图象在第一象限内有公共点时![]() 的取值范围;从“代数”角度考虑,应看作方程 有正数解时
的取值范围;从“代数”角度考虑,应看作方程 有正数解时![]() 的取值范围.
的取值范围.
(画图观察)
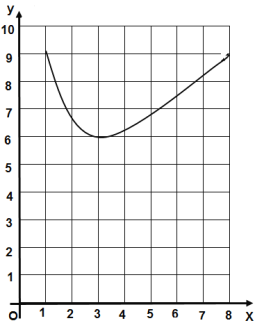
(2)函数![]() 的图象如图所示,而函数
的图象如图所示,而函数![]() 的图象是一条与
的图象是一条与![]() 轴平行的直线.当直线
轴平行的直线.当直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 唯一公共点( , )时,周长
唯一公共点( , )时,周长![]() 取得最小值为 .
取得最小值为 .
(代数说理)
(3)圆圆说矩形的周长可以为![]() ,方方说矩形的周长可以为
,方方说矩形的周长可以为![]() ,你认为圆圆和方方的说法对吗?为什么?
,你认为圆圆和方方的说法对吗?为什么?
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ;(3)矩形的周长为
;(3)矩形的周长为![]() ,方方的说法对,理由见解析
,方方的说法对,理由见解析
【解析】
(1)此题要读懂题意,从图形的角度去考虑应该是两条函数图象:![]() 与
与![]() 的图象在第一象限内有公共点时
的图象在第一象限内有公共点时![]() 的取值范围;从“代数”角度考虑,应看作方程
的取值范围;从“代数”角度考虑,应看作方程![]() 有正数解时
有正数解时![]() 的取值范围;
的取值范围;
(2)画出直线![]() 与
与![]() 有唯一公共点(3,6)即可解答问题;
有唯一公共点(3,6)即可解答问题;
(3)由(2)可知此矩形周长最小值为12,故圆圆的说法错误,方方的说法是有理的,可以通过解方程进行说明.
解(1)![]() ;
;![]()
(2)如图,

由图象可以看出,直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 唯一公共点(3,6),周长最小值为:
唯一公共点(3,6),周长最小值为:![]() ,即m=12;
,即m=12;
故答案为:![]() ,
,![]() ,
,![]() ;
;
(3)由(2)知,此矩形的周长最小值为12,圆圆说矩形的周长可以为![]() ,是错误的,方方说矩形的周长可以为
,是错误的,方方说矩形的周长可以为![]() ,是有道理的.
,是有道理的.
理由:若矩形的周长为![]()
则![]()
即![]()
整理,得![]()
![]()
![]() 方程
方程![]() 无解
无解
故矩形的周长不可能为![]() ,圆圆的说法不对
,圆圆的说法不对
若矩形的周长为![]()
则![]()
即![]()
整理,得![]()
![]()
![]() 方程
方程![]() 有两个不相等的实数根
有两个不相等的实数根
故矩形的周长为![]() ,方方的说法对
,方方的说法对


科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
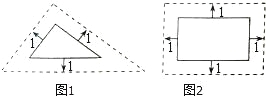
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
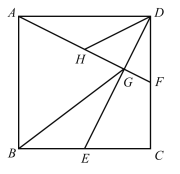
【题目】如图,在边长为4的正方形![]() 中,点
中,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 交于点
交于点![]() ,
,![]() 的中点为
的中点为![]() ,连接
,连接![]() 、
、![]() .给出下列结论:①
.给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有________.(请填上所有正确结论的序号)
.其中正确的结论有________.(请填上所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
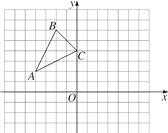
【题目】如图,已知A(-4,2),B(-2,6),C(0,4)是直角坐标系中的三点.
(1)把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1,画出平移后的图形,并写出点A的对应点A1的坐标;
(2)以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2,请在所给的坐标系中作出所有满足条件的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在平面直角坐标系中, ![]() 的顶点
的顶点![]() 与原点重合,点
与原点重合,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() 按以下步骤作图:①以点
按以下步骤作图:①以点![]() 为圆心,适当长度为半径作
为圆心,适当长度为半径作![]() 弧,分别交边
弧,分别交边![]() ,
,![]() 于点
于点![]() ,
,![]() ;②分别以点
;②分别以点![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧, 两弧在
的长为半径作弧, 两弧在![]() 内交于点
内交于点![]() ;③作射线
;③作射线![]() ,交边
,交边![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:(要求保留作图痕迹,不写作法)

(1)作△ABC中BC边上的垂直平分线EF(交AC于点E,交BC于点F);
(2)连结BE,若AC=10,AB=6,求△ABE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,![]() ,反比例函数
,反比例函数![]() 在第一象限的图象经过点B,则S△OAC-S△BAD=( )
在第一象限的图象经过点B,则S△OAC-S△BAD=( )
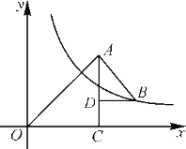
A.1.5B.2.5C.3D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节是中国的传统节日.今年端午节前夕,遂宁市某食品厂抽样调查了河东某居民区市民对A、B、C、D四种不同口味粽子样品的喜爱情况,并将调查情况绘制成如图两幅不完整统计图:
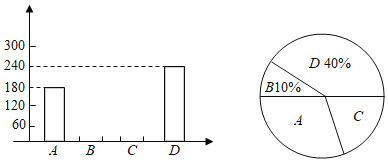
(1)本次参加抽样调查的居民有 人.
(2)喜欢C种口味粽子的人数所占圆心角为 度.根据题中信息补全条形统计图.
(3)若该居民小区有6000人,请你估计爱吃D种粽子的有 人.
(4)若有外型完全相同的A、B、C、D棕子各一个,煮熟后,小李吃了两个,请用列表或画树状图的方法求他第二个吃的粽子恰好是A种粽子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角是50度时,箱盖落在![]() 的位置(如图2),已知
的位置(如图2),已知![]()
![]()
![]()
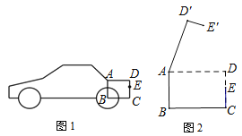
(1)求点![]() 到
到![]() 的距离;(结果保留整数)
的距离;(结果保留整数)
(2)求![]() 两点之间的距离.(结果保留整数)
两点之间的距离.(结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com