
【题目】已知:如图,一条直线上依次有A、B、C三点.
(1)若BC=60,AC=3AB,求AB的长;
(2)若点D是射线CB上一点,点M为BD的中点,点N为CD的中点,求![]() 的值;
的值;
(3)当点P在线段BC的延长线上运动时,点E是AP中点,点F是BC中点,下列结论中:
①![]() 是定值;
是定值;
②![]() 是定值.其中只有一个结论是正确的,请选择正确结论并求出其值.
是定值.其中只有一个结论是正确的,请选择正确结论并求出其值.

【答案】(1)AB=15;(2)2;(3)①见解析;②见解析.
【解析】
(1)由AC=AB+BC=3AB可得;
(2)分三种情况:①D在BC之间时②D在AB之间时③D在A点左侧时;
(3)分三种情况讨论:①F、E在BC之间,F在E左侧②F在BC之间,E在CP之间③F、E在BC之间,F在E右侧;
(1)∵BC=60,AC=AB+BC=3AB,
∴AB=15;
(2)∵点M为BD中点,点N为CD中点,
∴BM=BD,DN=NC,
①D在BC之间时:
![]()
BC=BD+CD=2MD+2DN=2MN,
∴![]() =2;
=2;
②D在AB之间时:
![]()
BC=DC﹣DB=2DN﹣2MB=2(BN+2MB)﹣2MB=2BN+2MB=2MN,
∴![]() =2;
=2;
③D在A点左侧时:
![]()
BC=DN+NB=MN+DN﹣NB=MN+MB﹣NB=MN+MN+NB﹣NB=2MN,
∴![]() =2;
=2;
故![]() =2;
=2;
(3)点E是AP的中点,点F是BC的中点.
∴AE=EP,BF=CF,
①
![]()
EF=FC﹣EC=![]() BC﹣AC+AE=
BC﹣AC+AE=![]() (AC﹣AB)﹣AC+AE=AE﹣
(AC﹣AB)﹣AC+AE=AE﹣![]() AB=
AB=![]() AC,
AC,
BP=AP﹣AB=2AE﹣AB,
AC﹣BP=AC﹣2AE+AB,
∴![]() =2.
=2.
②
![]()
EF=![]() BC+CE=
BC+CE=![]() BC+AE﹣AC=
BC+AE﹣AC=![]() (AC﹣AB)+AE﹣AC=AE﹣
(AC﹣AB)+AE﹣AC=AE﹣![]() AB﹣
AB﹣![]() AC,
AC,
BP=AP﹣AB=2AE﹣AB,
AC﹣BP=AC+AB﹣2AE,
∴![]() =2.
=2.
③
![]()
EF=CE﹣CF=CE﹣![]() BC=AC﹣AE﹣
BC=AC﹣AE﹣![]() BC=AC﹣AE﹣
BC=AC﹣AE﹣![]() (AC﹣AB)=
(AC﹣AB)=![]() AC﹣AE+
AC﹣AE+![]()
![]() AB,
AB,
BP=AP﹣AB=2AE﹣AB,
∴AC﹣BP=AC+AB﹣2AE,
∴![]() =2.
=2.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
【题目】请先阅读下列材料,再解答下列问题:
材料:因式分解:(x y)22(x y)1 .
解:将“ x y”看成整体,令 x y=A ,则
原式 A2A 1 ( A 1)2
再将“A”还原,得:原式 (x y 1)2 . 上述解题时用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法,请你解答下列问题:
(1)因式分解:(x y)26(x y) 9 = ;
(2)因式分解:(a b)(a b 4) 4 ;
(3)证明:若 n 为正整数,则式子(n 1)(n 2)(n23n) 1 的值一定是某一个整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )
A.2![]() ﹣2
﹣2
B.6
C.2![]() ﹣2
﹣2
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,A、B、C三点的坐标分别为(﹣2,4)、(﹣3,0)、(4,1).
(1)画出△ABC;
(2)△ABC的面积为 ;
(3)△ABC向上平移3个单位长度,向左平移1个单位长度.请画出图形并写出对应点A1B1C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,连接MC,将菱形ABCD翻折,使点A落在线段CM上的点E处,折痕交AB于点N,则线段EC的长为 . 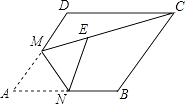
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】又到了一年中的春游季节.某班学生利用周末去参观“三军会师纪念塔”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.6m;
乙:我们相距36m.
请你根据两位同学的对话,计算纪念塔的高度.(精确到1米)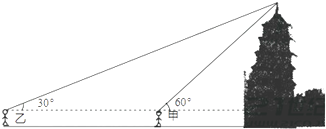
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条高铁线A,B,C三个车站的位置如图所示.已知B,C两站之间相距530千米.高铁列车从B站出发,向C站方向匀速行驶,经过13分钟距A站165千米;经过80分钟距A站500千米.
![]()
(1)求高铁列车的速度和AB两站之间的距离.(2)如果高铁列车从A站出发,开出多久可以到达C站?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(a,3),B(b,1)都在双曲线y= ![]() 上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com