
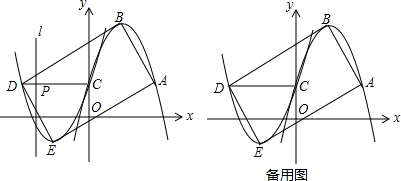
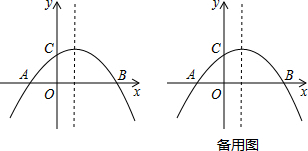
���� ��1��ֱ�ӽ���A���������y1=ax2-2ax+1�ó�m��ֵ����Ϊ��ͼ���֪��A�ڵ�һ���ޣ�����m��0����m=2��д��A��C�����꣬��D���A���ڵ�C�Գƣ��ɴ�д����D�����ꣻ
��2�����ݶ������깫ʽ�ó�������y1�Ķ���B�����꣬���ɾ��ζԽ��������ƽ�ֵã�BC=CD����ֱ�ǡ�BMC�У��ɹ��ɶ����з������a��ֵ�ó�������y1�Ľ���ʽ������ת�����ʵó�������y2�Ľ���ʽ��
��3��������������ۣ��ٵ�0��t��1ʱ��S=S��GHD=S��PDH+S��PDG���������߹���ֱ�������Σ����PG��PH�����������ʽ���㣻�ڵ�1��t��2ʱ��S=S��HMD��-S��GE��F-S��GE��M������30��Ǻ�60��ǵ�ֱ�������ε����ʽ��м���ó����ۣ�
��� �⣺��1��������ã�
��A��m��1������y1=ax2-2ax+1�ã�am2-2am+1=1��
��ã�m1=2��m2=0���ᣩ��
��A��2��1����C��0��1����D��-2��1����
��2����ͼ1���ɣ�1��֪��B��1��1-a��������B��BM��y�ᣬ
���ı���ABDEΪ���Σ���BC=CD��
��BM2+CM2=BC2=CD2��
��12+��-a��2=22��
��a=$��\sqrt{3}$��
��y1�����߿������£�
��a=-$\sqrt{3}$��
��y2��y1�Ƶ�C��ת180��õ�����E��-1��1-$\sqrt{3}$����
����y2=a��x+1��2+1-$\sqrt{3}$����a=$\sqrt{3}$��
��y2=$\sqrt{3}$x2+2$\sqrt{3}$x+1��
��3����ͼ1����0��t��1ʱ����DP=t������ֱ�ǡ�BQD��
��BQ=$\sqrt{3}$��DQ=3����BD=2$\sqrt{3}$��
���BDQ=30�㣬
��PH=$\frac{\sqrt{3}}{3}t$��PG=$\sqrt{3}$t��
��S=$\frac{1}{2}$��PG+PH����DP=$\frac{2\sqrt{3}}{3}$t2��
��ͼ2����1��t��2ʱ��
��Ϊ����ABDE��ֱ��l�۵��������ӳ�DE��D��E�佻ֱ��l��ͬһ�㣬����һ��ΪM��
D��-2��1����E��-1��1-$\sqrt{3}$����
��DE=$\sqrt{��-2+1��^{2}+��1-1+\sqrt{3}��^{2}}$=2��
��EM=DM-DE=2t-2��
�ߡ�EMG=30�㣬
��EG=E��G=$\frac{2\sqrt{3}}{3}$��t-1����
��Rt��FEM�У���EMF=2��30��=60�㣬
���EFM=30�㣬
��FM=2EM=4t-4��
��E��F=FM-E��M=FM-EM=4t-4-��2t-2��=2t-2=2��t-1����
S��GE��F=$\frac{2\sqrt{3}}{3}$��t-1��2��
S=S��HMD��-S��GE��F-S��GE��M=$\frac{1}{2}$��$\frac{2\sqrt{3}}{3}$t��2t-$\frac{2\sqrt{3}}{3}$��t-1��2-$\frac{1}{2}$��$\frac{2\sqrt{3}}{3}$��t-1������2t-2����
=-$\frac{2\sqrt{3}}{3}$${t}^{2}+\frac{8\sqrt{3}}{3}t-\frac{4\sqrt{3}}{3}$��
����������S=$\frac{2\sqrt{3}}{3}$t2��0��t��1����S=-$\frac{2\sqrt{3}}{3}$${t}^{2}+\frac{8\sqrt{3}}{3}t-\frac{4\sqrt{3}}{3}$��1��t��2����
���� ���⿼���˶��κ��������ʣ���ת�����ʺ;��ζԽ��ߵ����ʣ��Լ����Ǻ���������ǵ�Ӧ�ã��ۺ��Խ�ǿ�����ڴ���֪���ھ����������DZ���Ĺؼ����������Լ�����εı߳����Խ�����ߵļнǣ��ó�30�㣬�Դ�Ϊͻ�ƿڣ�����Ҫ�ı߳���t��ʾ���ó�������ϵʽ�����Ȿ������˷������۵�˼�룬���ڶ��κ��������ý϶࣬Ӧ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
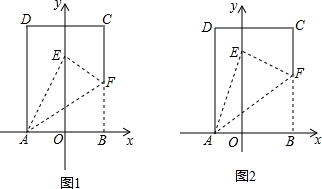 ��һ������ֽƬABCD���õ�ƽ��ֱ������ϵ�У���A��Bǡ����x��������������ϣ�������ֽƬ��AF�۵�����Bǡ������y���ϵĵ�E������OA=1��
��һ������ֽƬABCD���õ�ƽ��ֱ������ϵ�У���A��Bǡ����x��������������ϣ�������ֽƬ��AF�۵�����Bǡ������y���ϵĵ�E������OA=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 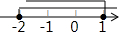 | B�� | 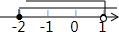 | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ߵij��� | B�� | �����ǵĶ��� | C�� | �����ε���� | D�� | �����ε��ܳ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a10-a7=a3 | B�� | ��-2a2b��2=-2a4b2 | C�� | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D�� | ��a+b��9�£�a+b��3=��a+b��6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
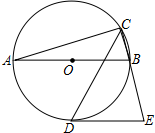 ��ͼ��AB�ǡѵ�ֱ����CD�ǡ�ACB��ƽ���߽���O�ڵ�D����D����O�����߽�CB���ӳ����ڵ�E����AB=4����E=75�㣬��CD�ij�Ϊ��������
��ͼ��AB�ǡѵ�ֱ����CD�ǡ�ACB��ƽ���߽���O�ڵ�D����D����O�����߽�CB���ӳ����ڵ�E����AB=4����E=75�㣬��CD�ij�Ϊ��������| A�� | $\sqrt{3}$ | B�� | 2 | C�� | 2$\sqrt{3}$ | D�� | 3$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com