
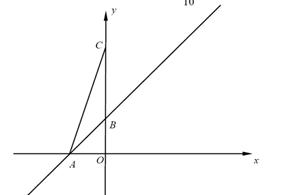
如图,一次函数 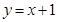 的图像与
的图像与 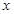 轴、
轴、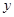 轴分别相交于点
轴分别相交于点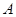 、
、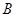 .二次函数的图像与
.二次函数的图像与 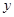 轴的正半轴相交于点
轴的正半轴相交于点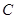 ,与这个一次函数的图像相交于点
,与这个一次函数的图像相交于点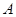 、
、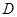 ,
,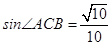 .
.
(1) 求点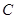 的坐标;
的坐标;
(2)如果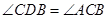 ,求这个二次函数的解析式.
,求这个二次函数的解析式.
(1)点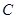 的坐标(0,3)(2)
的坐标(0,3)(2)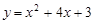
【解析】(1)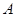 (
(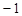 ,0),
,0),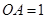 ,
(1分)
,
(1分)
在Rt△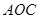 中,∵
中,∵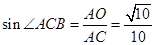 ,
,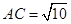 ,
(2分)
,
(2分)
∴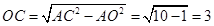 ,∴点
,∴点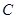 的坐标(0,3).
(1分)
的坐标(0,3).
(1分)
(2)当点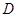 在
在 延长线上时,
延长线上时,
∵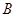 (0,1),
(0,1),
∴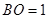 ,
,
∴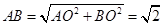 ,
,
∵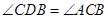 ,
,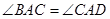 ,
,
∴△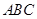 ∽△
∽△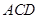 .
(1分)
.
(1分)
∴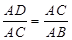 ,
,
∴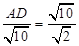 ,
,
∴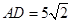 .
(1分)
.
(1分)
过点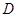 作
作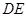 ⊥
⊥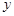 轴,垂足为
轴,垂足为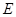 ,
,
∵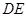 //
//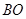 ,
,
∴ ,
,
∴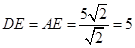 .
.
∴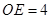 ,
,
∴点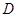 的坐标为(4,5).
(1分)
的坐标为(4,5).
(1分)
设二次函数的解析式为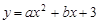 ,∴
,∴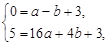 (1分)
(1分)
∴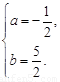
∴二次函数解析式为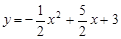 .
(1分)
.
(1分)
当点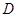 在射线
在射线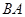 上时,同理可求得点
上时,同理可求得点 ,
(2分)
,
(2分)
二次函数解析式为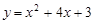 .
(1分)
.
(1分)
评分说明:过点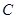 作
作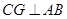 于
于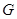 ,当点
,当点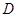 在
在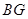 延长线上或点
延长线上或点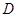 在射线
在射线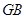 上时,可用锐
上时,可用锐
角三角比等方法得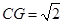 (1分),
(1分),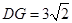 (1分),另外分类有1分其余同上.
(1分),另外分类有1分其余同上.
(1)先求出A点坐标为(-1,0),B点坐标为(0,1),则OA=1,OB=1,AB=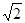 ,再根据正弦的定义得sin∠ACB=
,再根据正弦的定义得sin∠ACB=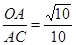 ,而AC=
,而AC=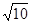 ,则OA=
,则OA=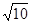 ,然后根据勾股定理可计算出OC=3,从而确定点C的坐标为(0,3);
,然后根据勾股定理可计算出OC=3,从而确定点C的坐标为(0,3);
(2)分类讨论:当点D在AB延长线上时,如图1,过点D作DE⊥y轴,垂足为E,由于∠CDB=∠ACB,∠BAC=∠CAD,根据相似的判定得△ABC∽△ACD,则AD:AC=AC:AB,即AD: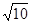 =
=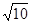 :
: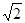 ,可计算出AD=5
,可计算出AD=5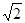 ,易得ADE为等腰直角三角形,则DE=AE=
,易得ADE为等腰直角三角形,则DE=AE=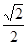 AD=
AD=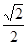 ×5
×5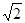 =5,OE=4,得到点D的坐标为(4,5),然后设一般式,利用待点系数法求过A(-1,0)、C(0,3)、D(4,5)的二次函数的解析式;当点D在射线BA上,如图2,过点D作DE⊥y轴,垂足为E,与前面的解法相同.
=5,OE=4,得到点D的坐标为(4,5),然后设一般式,利用待点系数法求过A(-1,0)、C(0,3)、D(4,5)的二次函数的解析式;当点D在射线BA上,如图2,过点D作DE⊥y轴,垂足为E,与前面的解法相同.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
 如图,已知反比例函数y=
如图,已知反比例函数y=| 12 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一次函数的图象与反比例函数![]() (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当x<-1时,一次函数值大于反比例函数值,当x>-1时,一次函数值小于反比例函数值.
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当x<-1时,一次函数值大于反比例函数值,当x>-1时,一次函数值小于反比例函数值.
(1)求一次函数的解析式;
(2)设函数![]() (x>0)的图象与
(x>0)的图象与![]() (x<0)的图象关于y轴对称,在
(x<0)的图象关于y轴对称,在![]() (x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
(x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一次函数的图象与反比例函数![]() (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当x<-1时,一次函数值大于反比例函数值,当x>-1时,一次函数值小于反比例函数值.
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当x<-1时,一次函数值大于反比例函数值,当x>-1时,一次函数值小于反比例函数值.
(1)求一次函数的解析式;
(2)设函数![]() (x>0)的图象与
(x>0)的图象与![]() (x<0)的图象关于y轴对称,在
(x<0)的图象关于y轴对称,在![]() (x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点
(x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点![]() 的坐标.
的坐标.
 解答:
解答:
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一次函数的图象与反比例函数![]() (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当x<-1时,一次函数值大于反比例函数值,当x>-1时,一次函数值小于反比例函数值.
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当x<-1时,一次函数值大于反比例函数值,当x>-1时,一次函数值小于反比例函数值.
(1)求一次函数的解析式;
(2)设函数![]() (x>0)的图象与
(x>0)的图象与![]() (x<0)的图象关于y轴对称,在
(x<0)的图象关于y轴对称,在![]() (x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点
(x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点![]() 的坐标.
的坐标.

查看答案和解析>>
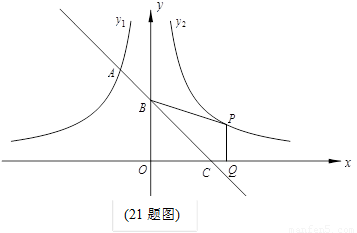
科目:初中数学 来源:2011年初中毕业升学考试(江苏扬州卷)数学 题型:解答题
如图,一次函数的图象与反比例函数y1= – ( x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<–1时,一次函数值大于反比例函数的值,当x>–1时,一次函数值小于反比例函数值.
(1) 求一次函数的解析式;
(2) 设函数y2= (x>0)的图象与y1= – (x<0)的图象关于y轴对称.在y2= (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com