
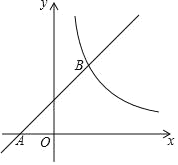
【题目】如图,在平面直角坐标系xOy中,一次函数y=x+b的图象经过点A(﹣2,0),与反比例函数y=![]() (x>0)的图象交于B(a,4).
(x>0)的图象交于B(a,4).
(1)求一次函数和反比例函数的表达式;
(2)设M(m﹣2,m)是直线AB上一点,过M作MN∥x轴,交反比例函数y=![]() (x>0)的图象于点N,若AONM为顶点的四边形为平行四边形,求点M的坐标.
(x>0)的图象于点N,若AONM为顶点的四边形为平行四边形,求点M的坐标.
【答案】(1)y=x+2,![]() ;(2)点M的坐标为
;(2)点M的坐标为![]() .
.
【解析】
(1)用待定系数法求解;(2)由题意可知M(m﹣2,m),点N(![]() ,m),当MN∥AO且MN=AO=2时,四边形AONM是平行四边形,则
,m),当MN∥AO且MN=AO=2时,四边形AONM是平行四边形,则![]() ﹣(m﹣2)=±2,求解即可.
﹣(m﹣2)=±2,求解即可.
解:(1)∵一次函数y=x+b的图象经过点A(﹣2,0),
∴0=﹣2+b,得b=2,
∴一次函数的解析式为y=x+2,
∵一次函数的解析式为y=x+2与反比例函数y=![]() (x>0)的图象交于B(a,4),
(x>0)的图象交于B(a,4),
∴4=a+2,得a=2,
∴4=![]() ,得k=8,
,得k=8,
即反比例函数解析式为:y=![]() (x>0);
(x>0);
(2)∵点A(﹣2,0),
∴OA=2,
由题意可知M(m﹣2,m),点N(![]() ,m),
,m),
当MN∥AO且MN=AO=2时,四边形AONM是平行四边形,
![]() ﹣(m﹣2)=±2
﹣(m﹣2)=±2
解得,m=2 ![]() ,或m=2
,或m=2 ![]() +2(舍弃)(负值已舍去)
+2(舍弃)(负值已舍去)
∴点M的坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】观察思考:

(1)在∠AOB内部画1条射线OC,则图中有3个不同的角;
(2)在∠AOB内部画2条射线OC、OD,则图中有几个不同的角?
(3)3条射线呢?你能发现什么规律,表示出n条射线能有几个不同的角?
请你先解答以上问题,再结合已学过的知识,针对类似的图形也提出三个问题并作答.(要求:画出图形,写出题干,提出问题并作答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天上午,一出租车司机始终在一条南北走向的笔直马路上营运,(出发点记作为点O,约定向南为正,向北为负),期间一共运载6名乘客,行车里程(单位:千米)依先后次序记录如下:﹢7,﹣3,﹢6,﹣1,﹢2,﹣4.
(1)出租车在行驶过程中,离出发点O最远的距离是______千米;
(2)将最后一名乘客送到目的地,出租车离出发点O多远?在O点的什么方向?
(3)出租车收费标准为:起步价(不超过3千米)为8元,超过3千米的部分每千米的价格为1.5元,求司机这天上午的营业额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

A. 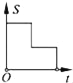 B.
B. 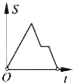 C.
C. 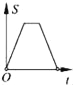 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
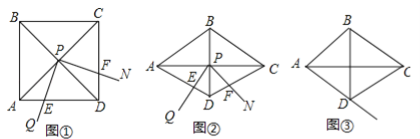
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是 ;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=![]() AD,请给出证明;
AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天快递配送员张强一直在一条南北走向的街道上送快递,如果规定向北为正,向南为负,这天他从出发点开始所走的路程(单位:![]() )记录如下:
)记录如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)这天送完最后一个快递时,张强在出发点的什么方向?距离出发点有多远?
(2)如果张强送完快递时,需立刻返回出发点,那么他这天送快递(含返回)共耗油多少升(每千米耗油![]() )?
)?
查看答案和解析>>
科目:初中数学 来源: 题型:
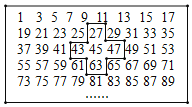
【题目】如图,将连续的奇数1,3,5,7……排成如下的数表,用十字形框框出5个数.
探究规律一:设十字框中间的奇数为x,则框中五个奇数的和用含x的整式表示为 ,这说明被十字框框中的五个奇数的和一定是正整数n(n>1)的倍数,这个正整数n是 ;
探究规律二:落在十字框中间且位于第二列的一组奇数是21,39,57,75,…,则这一组数可以用整式表示为18m+3(m为序数),同样,落在十字框中间且位于第三列的一组奇数可以表示为 ;(用含m的式子表示)
运用规律:
(1)已知被十字框框中的五个奇数的和为2025,则十字框中间的奇数是 ,这个奇数落在从左往右第 列;
(2)被十字框框中的五个奇数的和可能是2020吗?若能,请求出这五个数:若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路的路基是等腰梯形ABCD,斜坡AD、BC的坡度i=1:1.5,路基AE高为3米,现由单线改为复线,路基需加宽4米,(即AH=4米),加宽后也成等腰梯形,且GH、BF斜坡的坡度i'=1:2,若路长为10000米,则加宽的土石方量共是____立方米.
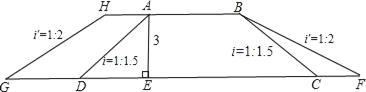
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com