
Ζ÷Έω Θ®1Θ©…ηΟΩΝΨ–ΓΩΆ≥ΒΡήΉχx»ΥΘ§ΟΩΝΨ¥σΩΆ≥ΒΡήΉχy»ΥΘ§ΗυΨίΧβ“βΩ…ΒΟΒ»ΝΩΙΊœΒΘΚ3ΝΨ–ΓΩΆ≥ΒΉυΒΡ»Υ ΐ+1ΝΨ¥σΩΆ≥ΒΉυΒΡ»Υ ΐ=105»ΥΘΜ1ΝΨ–ΓΩΆ≥ΒΉυΒΡ»Υ ΐ+2ΝΨ¥σΩΆ≥ΒΉυΒΡ»Υ ΐ=110»ΥΘ§ΗυΨίΒ»ΝΩΙΊœΒΝ–≥ωΖΫ≥ΧΉιΘ§‘ΌΫβΦ¥Ω…ΘΜ
Θ®2Θ©ΔΌΗυΨίΧβ“βΩ…ΒΟ–ΓΩΆ≥ΒmΝΨ‘ΥΒΡ»Υ ΐ+¥σΩΆ≥ΒnΝΨ‘ΥΒΡ»Υ ΐ=400Θ§»ΜΚσ«σ≥ω’ϊ ΐΫβΦ¥Ω…ΘΜ
ΔΎΗυΨίΔΌΥυΒΟΖΫΑΗΚΆ–ΓΩΆ≥ΒΟΩΝΨΉβΫπ150‘ΣΘ§¥σΩΆ≥ΒΟΩΝΨΉβΫπ250‘ΣΖ÷±πΦΤΥψ≥ωΉβΫπΦ¥Ω…Θ°
Ϋβ¥π Θ®1Θ©…η1ΝΨ–ΓΩΆ≥Β“Μ¥ΈΩ…ΥΆ―ß…ζx»ΥΘ§1ΝΨ¥σΩΆ≥ΒΕΦΉχ¬ζΚσ“Μ¥ΈΩ…ΥΆyΟϊ―ß…ζΘ§
”…Χβ“βΒΟΘΚ$\left\{\begin{array}{l}3x+y=105\\ x+2y=110\end{array}\right.$Θ§
ΫβΒΟΘΚ$\left\{\begin{array}{l}x=20\\ y=45\end{array}\right.$Θ§
¥πΘΚ1ΝΨ–ΓΩΆ≥ΒΉχ20»ΥΘ§1ΝΨ¥σΩΆ≥ΒΉχ45»ΥΘ°
Θ®2Θ©…ηΉβ–ΓΩΆ≥ΒaΝΨΘ§¥σΩΆ≥ΒbΝΨΘ§”…Χβ“βΒΟΘΚ
20a+45b=400Θ§
ΓΏΟΩΝΨΤϊ≥Β«ΓΚΟΕΦΉχ¬ζΘ§
ΓύaΓΔbΒΡ÷ΒΨυΈΣΖ«ΗΚ’ϊ ΐΘ§
ΓύaΓΔbΩ…»Γ$\left\{\begin{array}{l}a=20\\ b=0\end{array}\right.$Θ§$\left\{\begin{array}{l}a=11\\ b=4\end{array}\right.$Θ§$\left\{\begin{array}{l}a=2\\ b=8\end{array}\right.$
¥πΘΚΙ≤”–3÷÷Ήβ≥ΒΖΫΑΗΘ°ΔΌΖ÷±π «Ήβ–Γ≥Β20ΝΨΘ§≤ΜΉβ¥σ≥ΒΘΜΔΎΉβ–Γ≥Β11ΝΨΘ§Ήβ¥σ≥Β4ΝΨΘΜΔέΉβ–Γ≥Β2ΝΨΘ§Ήβ¥σ≥Β8ΝΨΘΜ
Θ®3Θ©ΖΫΑΗ1ΉβΫπΈΣΘΚ250ΓΝ20=5000Θ®‘ΣΘ©ΘΜ
ΖΫΑΗ2ΉβΫπΈΣΘΚ250ΓΝ11+350ΓΝ4=4150Θ®‘ΣΘ©ΘΜ
ΖΫΑΗ3ΉβΫπΈΣΘΚ250ΓΝ2+350ΓΝ8=3300Θ®‘ΣΘ©Θ°
¥πΘ§ΖΫΑΗ3Ήν Γ«°Θ§–η“Σ3300‘ΣΘ°
ΒψΤά ¥ΥΧβ÷ς“ΣΩΦ≤ιΝΥΕΰ‘Σ“Μ¥ΈΖΫ≥ΧΉιΒΡ”Π”ΟΘ§ΙΊΦϋ «’ΐ»ΖάμΫβΧβ“βΘ§’“≥ωΧβΡΩ÷–ΒΡΒ»ΝΩΙΊœΒΘ§Ν–≥ωΕΰ‘Σ“Μ¥ΈΖΫ≥ΧΜρΖΫ≥ΧΉιΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\sqrt{\frac{1}{3}}$ | BΘ° | $\sqrt{{m}^{2}+1}$ | CΘ° | $\sqrt{{a}^{3}}$Θ®aΘΨ0Θ© | DΘ° | $\sqrt{8}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 3a3-2a2=0 | BΘ° | a3•a${\;}^{\frac{1}{3}}$=a | CΘ° | a3Γ¬a2=a | DΘ° | Θ®a2Θ©${\;}^{\frac{1}{2}}$=a${\;}^{\frac{5}{2}}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
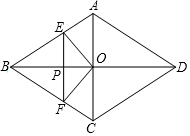 »γΆΦΘ§Νβ–ΈABCDΒΡΕ‘Ϋ«œΏAC”κBDΫΜ”ΎΒψOΘ§AC=6Θ§BD=8Θ°Ε·ΒψE¥”ΒψB≥ωΖΔΘ§―ΊΉ≈B-A-D‘ΎΝβ–ΈABCDΒΡ±Ώ…œ‘ΥΕ·Θ§‘ΥΕ·ΒΫΒψDΆΘ÷ΙΘ°ΒψF «ΒψEΙΊ”ΎBDΒΡΕ‘≥ΤΒψΘ§EFΫΜBD”ΎΒψPΘ§»τBP=xΘ§ΓςOEFΒΡΟφΜΐΈΣyΘ§‘ρy”κx÷°ΦδΒΡΚ· ΐΆΦœσ¥σ÷¬ΈΣΘ®ΓΓΓΓΘ©
»γΆΦΘ§Νβ–ΈABCDΒΡΕ‘Ϋ«œΏAC”κBDΫΜ”ΎΒψOΘ§AC=6Θ§BD=8Θ°Ε·ΒψE¥”ΒψB≥ωΖΔΘ§―ΊΉ≈B-A-D‘ΎΝβ–ΈABCDΒΡ±Ώ…œ‘ΥΕ·Θ§‘ΥΕ·ΒΫΒψDΆΘ÷ΙΘ°ΒψF «ΒψEΙΊ”ΎBDΒΡΕ‘≥ΤΒψΘ§EFΫΜBD”ΎΒψPΘ§»τBP=xΘ§ΓςOEFΒΡΟφΜΐΈΣyΘ§‘ρy”κx÷°ΦδΒΡΚ· ΐΆΦœσ¥σ÷¬ΈΣΘ®ΓΓΓΓΘ©| AΘ° | 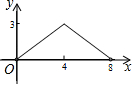 | BΘ° | 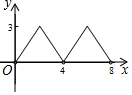 | CΘ° | 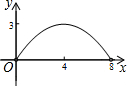 | DΘ° |  |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° |  | BΘ° |  | ||
| CΘ° |  | DΘ° |  |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
 “―÷ΣΘΚ»γΆΦΘ§OΈΣΓ―OΒΡ‘≤–ΡΘ§ΒψD‘ΎΓ―O…œΘ§»τΓœAOC=110ΓψΘ§‘ρΓœADCΒΡΕ» ΐΈΣΘ®ΓΓΓΓΘ©
“―÷ΣΘΚ»γΆΦΘ§OΈΣΓ―OΒΡ‘≤–ΡΘ§ΒψD‘ΎΓ―O…œΘ§»τΓœAOC=110ΓψΘ§‘ρΓœADCΒΡΕ» ΐΈΣΘ®ΓΓΓΓΘ©| AΘ° | 55Γψ | BΘ° | 110Γψ | CΘ° | 125Γψ | DΘ° | 72.5Γψ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com