
已知双曲线 上一点M(1,m)和双曲线
上一点M(1,m)和双曲线 上一点N(n,3).
上一点N(n,3).
(1)求m、n的值;
(2)求△OMN的面积.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
如图,点A,B分别在 轴,
轴,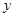 轴上,点D在第一象限内,DC⊥
轴上,点D在第一象限内,DC⊥ 轴于点C,AO=CD=2,AB=DA=
轴于点C,AO=CD=2,AB=DA= ,反比例函数
,反比例函数 的图象过CD的中点E。
的图象过CD的中点E。
(1)求证:△AOB≌△DCA;
(2)求 的值;
的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在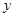 轴上,试判断点G是否在反比例函数的图象上,并说明理由。(
轴上,试判断点G是否在反比例函数的图象上,并说明理由。(
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,O为坐标原点,P是反比例函数 (x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(1)求证:线段AB为⊙P的直径;
(2)求△AOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,反比例函数 的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
(1)求一次函数的表达式;
(2)观察图象,直接写出使反比例函数值大于一次函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图在平面直角坐标系xOy中,函数 (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年浙江义乌12分)如图1,已知 (x>
(x> )图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
(1)如图2,连结BP,求△PAB的面积;
(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为 ,求此时P点的坐标;
,求此时P点的坐标;
(3)当点Q在射线BD上时,且a=3,b=1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
为响应国家要求中小学生每天锻练1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的图1和图2
【小题1】求被调查的班级的学生人数
【小题2】求喜欢“乒乓球”的学生人数,并在图1中将“乒乓球”部分的图形补充完整;
【小题3】若该校共有2000名学生,请估计喜欢“足球”的学生人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com