
 如图,在△ABC中,AD⊥BC,垂足为D,AD=4,BD=2,CD=8.
如图,在△ABC中,AD⊥BC,垂足为D,AD=4,BD=2,CD=8.分析 (1)在Rt△ABD中利用勾股定理可求AB2,同理在Rt△ACD中利用勾股定理可求AC2,而BC=CD+BD=10,易求AC2+AB2=100=BC2,从而可知△ABC是直角三角形.
(2)分三种情况:①当BP=AB时;②当BP=AP时;③当AP=AB时;分别求出BP的长即可.
解答 (11)证明:△ABC是直角三角形,理由如下:
∵AD⊥BC,AD=4,BD=2,
∴AB2=AD2+BD2=20,
又∵AD⊥BC,CD=8,AD=4,
∴AC2=CD2+AD2=80,
∵BC=CD+BD=10,
∴BC2=100,
∴AC2+AB2=100=BC2,
∴∠BAC=90°,△ABC是直角三角形.
(2)解:分三种情况:
①当BP=AB时,
∵AD⊥BC,
∴AB=$\sqrt{B{D}^{2}+A{D}^{2}}$=2$\sqrt{5}$,
∴BP=AB=2$\sqrt{5}$;
②当BP=AP时,P我BC的中点,
∴BP=$\frac{1}{2}$AB=5;
③当AP=AB是,BP=2BD=4;
综上所述:BP的长为2$\sqrt{5}$或5或4.
点评 本题考查勾股定理、勾股定理的逆定理的应用以及等腰三角形的性质.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
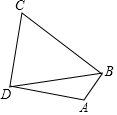 已知:在四边形ABCD中,∠ABC=90°,∠C=60,AB=$\frac{\sqrt{3}}{2}$,BC=1+$\sqrt{3}$,CD=2
已知:在四边形ABCD中,∠ABC=90°,∠C=60,AB=$\frac{\sqrt{3}}{2}$,BC=1+$\sqrt{3}$,CD=2查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=mx2-4mx+4m+3的顶点为A.
在平面直角坐标系xOy中,抛物线y=mx2-4mx+4m+3的顶点为A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com