
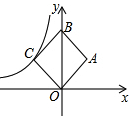
 如图,在平面直角坐标系中,正方形OABC的面积为24,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k=-12.
如图,在平面直角坐标系中,正方形OABC的面积为24,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k=-12. 分析 连接CA交y轴于点D,如图,先利用正方形的性质得AC⊥OB,S△OCD=$\frac{1}{4}$S正方形ABCO=6,再根据反比例函数k的几何意义得到$\frac{1}{2}$|k|=6,然后取绝对值即可得到满足条件的k的值.
解答 解: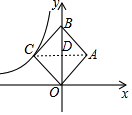 连接CA交y轴于点D,如图,
连接CA交y轴于点D,如图,
∵四边形ABCO为正方形,
∴AC⊥OB,S△OCD=$\frac{1}{4}$S正方形ABCO=$\frac{1}{4}$×24=6,
∵$\frac{1}{2}$|k|=6,
而k<0,
∴k=-12.
故答案为-12.
点评 本题考查了反比例函数系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
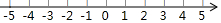 解不等式组$\left\{\begin{array}{l}{2(x+1)≥0,①}\\{1-\frac{x}{3}>\frac{x-3}{6},②}\end{array}\right.$并把解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{2(x+1)≥0,①}\\{1-\frac{x}{3}>\frac{x-3}{6},②}\end{array}\right.$并把解集在数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 菱形的对角线相等且互相平分 | B. | 矩形的对角线相等且互相平分 | ||
| C. | 对角线互相垂直的四边形是菱形 | D. | 对角线相等的四边形是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
如图所示,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
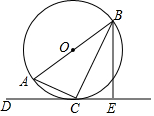 AB是⊙O的直径,CD切⊙O于点C,BE⊥CD于E,连接AC、BC.
AB是⊙O的直径,CD切⊙O于点C,BE⊥CD于E,连接AC、BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com