
已知,点P(x,y)在第一象限,且x+y=12,点A(10,0)在x轴上,设△OPA的面积 为S.
1.求S关于x 的关系式,并确定x的取值范围;
2.当△OPA为直角三角形时,求P点的坐标.


1.由 x+y=12得, .
.
即P(x,y)在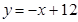 的函数图象上,且在第一象限.
的函数图象上,且在第一象限.
过点P作PB⊥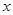 轴,垂足为B.
轴,垂足为B.
则 S△OPA= =
= =
= .
.
且0<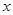 <12 ;
<12 ;
2.分情况讨论:
①若O为直角顶点,则点P在 轴上,不合题意舍去;
轴上,不合题意舍去;
②若A为直角顶点,则PA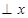 轴,所以点P的横坐标为10,代入
轴,所以点P的横坐标为10,代入 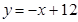 中,
中,
得 ,所以点P坐标(10, 2);
,所以点P坐标(10, 2);
③若P为直角顶点,可得△OPB∽△PAB .
∴ .
∴PB 2= OB·OA .
.
∴PB 2= OB·OA .
∴ .
.
解得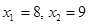 .
.
∴点P坐标(8, 4)或(9,3)
所以当△OPA为直角三角形时,点P的坐标为(10, 2)或(8, 4)或(9, 3).
【解析】此题注意第(2)分情况讨论,三个点都有可能是直角顶点,根据三角形相似,找出边和边之间的关系,列出方程求解。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
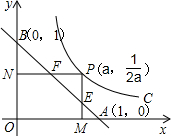 如图,已知动点P在函数y=
如图,已知动点P在函数y=| 1 |
| 2x |
| A、4 | ||
| B、2 | ||
| C、1 | ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
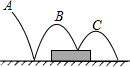 一个有弹性的球从A点落下到地面,弹起后,到B点又落到高为20cm的平台上,再弹起到C点,然后,又落到地面(如图),每次弹起的高度为落下高度的
一个有弹性的球从A点落下到地面,弹起后,到B点又落到高为20cm的平台上,再弹起到C点,然后,又落到地面(如图),每次弹起的高度为落下高度的| 4 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com