
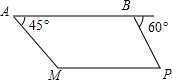
 如图,我巡逻机在海岛M上空巡逻,距离海平面垂直高度为1000米,在A点测得正前方海岛M的俯角为45°,在沿海面水平方向飞行2000米到达B点时测得一不明船只P的俯角为60°,已知A,B,P,M在同一水平面上,求不明船只P与海岛M之间的距离(结果保留根号)
如图,我巡逻机在海岛M上空巡逻,距离海平面垂直高度为1000米,在A点测得正前方海岛M的俯角为45°,在沿海面水平方向飞行2000米到达B点时测得一不明船只P的俯角为60°,已知A,B,P,M在同一水平面上,求不明船只P与海岛M之间的距离(结果保留根号) 分析 过M作MC⊥AB于C,PD⊥AB于D,在Rt△ACM中,求得AC=1000,在Rt△PBD中,求得BD=$\frac{1000\sqrt{3}}{3}$,于是得到结论.
解答 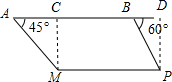 解:过M作MC⊥AB于C,PD⊥AB于D,
解:过M作MC⊥AB于C,PD⊥AB于D,
在Rt△ACM中,∠MAC=45°CM=1000,
∴AC=1000,
在Rt△PBD中,∠PBD=60°,PD=1000,
∴tan60°=$\frac{1000}{BD}$,
解得:BD=$\frac{1000\sqrt{3}}{3}$,
∴PM=CD=2000+$\frac{1000\sqrt{3}}{3}$-1000=1000+$\frac{1000\sqrt{3}}{3}$,
∴不明船只P与海岛M之间的距离为91000+$\frac{1000\sqrt{3}}{3}$)m.
点评 此题考查了俯角的定义、解直角三角形与矩形的性质.注意能借助俯角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60° | B. | 90° | C. | 135° | D. | 180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
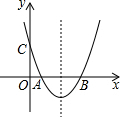 如图,关于x的二次函数y=x2-x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a-1)x+m的图象可能是( )
如图,关于x的二次函数y=x2-x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a-1)x+m的图象可能是( )| A. | 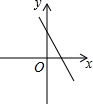 | B. | 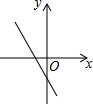 | C. | 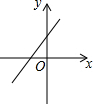 | D. | 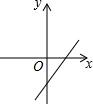 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
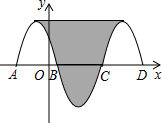 如图,抛物线y=-x2-2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为32.
如图,抛物线y=-x2-2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为32.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
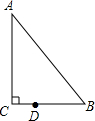 如图,在△ABC中,∠C=90°,∠B=55°,点D在BC边上,DB=2CD,若将△ABC绕点D逆时针旋转α度(0<α<180)后,点B恰好落在初始位置时△ABC的边上,则α等于70或120.
如图,在△ABC中,∠C=90°,∠B=55°,点D在BC边上,DB=2CD,若将△ABC绕点D逆时针旋转α度(0<α<180)后,点B恰好落在初始位置时△ABC的边上,则α等于70或120.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com