练习册

  • 练习册
  • 试题
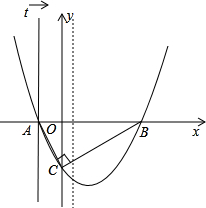    精英家教网 > 初中数学 > 题目详情
    如图所示，由三个正方体木块粘合成的模型，它们的棱长分别为1米、2米、4米，要在表面积上涂刷漆，若大正方体的下底面不涂油漆，则模型涂刷油漆的总面积为
    100
    100
    平方米．
    分析：观察模型形状可知，求出棱长为4米的正方体5个面的面积和棱长分别为1米、2米的正方体4个面的面积之和即为模型涂刷油漆的总面积．
    解答：解：1米的正方体4个面的面积是：4平方米，
    2米的正方体4个面的面积是：16平方米，
    4米的正方体5个面的面积是：80平方米，
    此模型涂刷油漆的总面积：4+16+80=100平方米，
    故答案为100．
    点评：本题主要考查面积及等积变换的知识，此题比较简单，但是也是比较容易出错，可能会把正方体的面积多加或者少加，解答时必须细心．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在平面直角示系中，A、B两点的坐标分别是A（-1，0）、B（4，0），点C在精英家教网y轴的负半轴上，且∠ACB=90°
    （1）求点C的坐标；
    （2）求经过A、B、C三点的抛物线的解析式；
    （3）直线l⊥x轴，若直线l由点A开始沿x轴正方向以每秒1个单位的速度匀速向右平移，设运动时间为t（0≤t≤5）秒，运动过程中直线l在△ABC中所扫过的面积为S，求S与t的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源：第2章《二次函数》中考题集（27）：2.7 最大面积是多少（解析版） 题型：解答题

    如图，在平面直角示系中，A、B两点的坐标分别是A（-1，0）、B（4，0），点C在y轴的负半轴上，且∠ACB=90°
    （1）求点C的坐标；
    （2）求经过A、B、C三点的抛物线的解析式；
    （3）直线l⊥x轴，若直线l由点A开始沿x轴正方向以每秒1个单位的速度匀速向右平移，设运动时间为t（0≤t≤5）秒，运动过程中直线l在△ABC中所扫过的面积为S，求S与t的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源：第2章《二次函数》中考题集（30）：2.3 二次函数的应用（解析版） 题型：解答题

    如图，在平面直角示系中，A、B两点的坐标分别是A（-1，0）、B（4，0），点C在y轴的负半轴上，且∠ACB=90°
    （1）求点C的坐标；
    （2）求经过A、B、C三点的抛物线的解析式；
    （3）直线l⊥x轴，若直线l由点A开始沿x轴正方向以每秒1个单位的速度匀速向右平移，设运动时间为t（0≤t≤5）秒，运动过程中直线l在△ABC中所扫过的面积为S，求S与t的函数关系式．

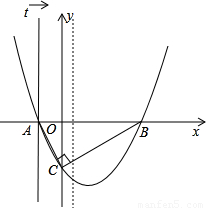
    查看答案和解析>>

    科目：初中数学 来源：第6章《二次函数》中考题集（30）：6.4 二次函数的应用（解析版） 题型：解答题

    如图，在平面直角示系中，A、B两点的坐标分别是A（-1，0）、B（4，0），点C在y轴的负半轴上，且∠ACB=90°
    （1）求点C的坐标；
    （2）求经过A、B、C三点的抛物线的解析式；
    （3）直线l⊥x轴，若直线l由点A开始沿x轴正方向以每秒1个单位的速度匀速向右平移，设运动时间为t（0≤t≤5）秒，运动过程中直线l在△ABC中所扫过的面积为S，求S与t的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源：2010年云南省丽江中考数学试卷（解析版） 题型：解答题

    （2010•丽江）如图，在平面直角示系中，A、B两点的坐标分别是A（-1，0）、B（4，0），点C在y轴的负半轴上，且∠ACB=90°
    （1）求点C的坐标；
    （2）求经过A、B、C三点的抛物线的解析式；
    （3）直线l⊥x轴，若直线l由点A开始沿x轴正方向以每秒1个单位的速度匀速向右平移，设运动时间为t（0≤t≤5）秒，运动过程中直线l在△ABC中所扫过的面积为S，求S与t的函数关系式．

    查看答案和解析>>

    同步练习册答案