
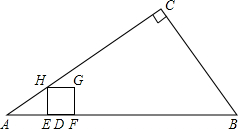
 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在AB上,AD=2cm.点E、F同时从点D出发,点E沿DA以1cm每秒的速度向点A运动,到达A点后立即以原速度沿AB向点B匀速运动;点F沿DB以2cm每秒的速度向点B匀速运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在AB上,AD=2cm.点E、F同时从点D出发,点E沿DA以1cm每秒的速度向点A运动,到达A点后立即以原速度沿AB向点B匀速运动;点F沿DB以2cm每秒的速度向点B匀速运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分面积为S.分析 (1)根据题意可知:△AHE∽△ACB,利用相似三角形的性质可知:$\frac{HE}{BC}$=$\frac{AE}{AC}$,从而可求得t的值;
(2)①当0<t≤$\frac{2}{5}$时,重合部分的面积等于正方形的面积;②当$\frac{2}{5}$<t≤1时,S=S正方形EFGH-S△MNH;③如图4,当1<t≤2时,S=S△ANF-S△AEM;
(3)如图5所示:过点N作NG⊥AB,垂足为G.根据勾股定理求得EN、FN,EF的长用函数t的代数式表示,然后分为①NE=NF;②EN=EF时;③当NF=EF三种情况计算即可.
解答 解:(1)当点E由D向A运动过程中,即当0<t<2时,如图1,
HE=3t,AE=2-t
∵△AHE∽△ACB,
∴$\frac{HE}{BC}$=$\frac{AE}{AC}$,即:$\frac{3t}{6}$=$\frac{2-t}{8}$,解得t=$\frac{2}{5}$;
(2)①当0<t≤$\frac{2}{5}$时,S与t的函数关系式是:S=3t×3t=9t2;
②如图2,当点G落在AC上时,GF=3t,AF=2+2t
∵△AGF∽△ACB,
∴$\frac{AF}{AC}$=$\frac{GF}{BC}$,即$\frac{2+2t}{8}$=$\frac{3t}{6}$,解得t=1,
∴如图3,当$\frac{2}{5}$<t≤1时,
S=S正方形EFGH-S△MNH=9t2-$\frac{1}{2}$HN•HM=9t2-$\frac{1}{2}$[3t-(2-t)×$\frac{3}{4}$]×$\frac{4}{3}$×[3t-(2-t)×$\frac{3}{4}$]=-$\frac{3}{8}$t2+$\frac{15}{2}$t-$\frac{3}{2}$,
③如图4,当1<t≤2时,
AF=2t+2,FN=$\frac{3}{4}$(2t+2)=$\frac{3}{2}$(t+1),AE=2t+2-3t=2-t,ME=$\frac{3}{4}$(2-t),
S=S△ANF-S△AEM=$\frac{1}{2}$AF•FN-$\frac{1}{2}$AE•EM=$\frac{1}{2}$×(2t+2)×$\frac{3}{2}$(t+1)-$\frac{1}{2}$×(2-t)×$\frac{3}{4}$(2-t)=$\frac{9}{8}$t2-$\frac{9}{2}$t.
(3)当t≥2时,存在使△EGB为等腰三角形的t的值.
如图5所示:过点N作NG⊥AB,垂足为G.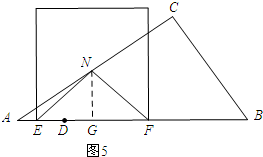
①当NE=NF时.
∵NE=NF,NG⊥EF,
∴EG=FG.
∵∠A=∠A,∠C=∠AGN,
∴△AGN∽△ACB.
∴$\frac{AN}{AB}=\frac{AG}{AC}$,即$\frac{4}{10}=\frac{AG}{8}$.
解得:AG=3.2.
∵AF=2+2t,
∴GF=2+2t-3.2=2t-1.2.
∴AE=AG-GE=3.2-(2t-1.2)=4.4-2t.
又∵AE=t-2,
∴4.4-2t=t-2.
解得:t=$\frac{32}{15}$.
②当EN=EF时,
由①可知:△AGN∽△ACB.
∴$\frac{AN}{AB}=\frac{GN}{BC}$,即$\frac{4}{10}=\frac{GN}{6}$.
解得:NG=2.4.
EG=AG-AE=3.2-(t-2)=5.2-t,
在Rt△EGN中,EN2=EG2+NG2,即EN2=(5.2-t)2+2.42,
EF=AF-AE=2+2t-(t-2)=4-t.
∴(5.2-t)2+2.42=(4-t)2.
解得:t=7(舍去),
③当NF=EF时,
由②知:NG=2.4,
FG=AF-AG=2+2t-3.2=2t-1.2.
NF2=NG2+GF2=(2t-1.2)2+2.42.
EF2=(4-t)2.
∴(2t-1.2)2+2.42=(4-t)2.
解得:${t}_{1}=\frac{-3.2+\sqrt{125.84}}{6}$,${t}_{2}=\frac{-3.2-\sqrt{125.84}}{6}$(舍去),
∵t1=$\frac{-3.2+\sqrt{125.84}}{6}$$<\frac{-3.2+12}{6}<2$(舍去).
综上所述,当t=$\frac{32}{15}$时,EN=FN,此时△EFN为等腰三角形.
点评 此题主要考查了动点函数问题,其中应用到了相似形、等腰三角形的性质、正方形及勾股定理的性质,分类思想的运用,锻炼了学生运用综合知识解答题目的能力.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明和小亮进行百米赛跑,小明比小亮跑得快.如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米.途中l1,l2分别表示两人所跑路程与时间的关系.根据图象回答:
小明和小亮进行百米赛跑,小明比小亮跑得快.如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米.途中l1,l2分别表示两人所跑路程与时间的关系.根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB>AC,已知点D是∠BAC的平分线上的点,过D作DE⊥AB于点E,作DF⊥AC于点F,∠ABD+∠ACD=180°.试着说明BD=DC.
如图,AB>AC,已知点D是∠BAC的平分线上的点,过D作DE⊥AB于点E,作DF⊥AC于点F,∠ABD+∠ACD=180°.试着说明BD=DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
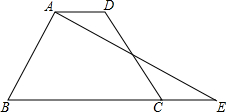 如图,在四边形ABCD中,点F是边CD上一点,连结AF,并延长AF交BC的延长线于点E,使得△ADF与△FCE全等.
如图,在四边形ABCD中,点F是边CD上一点,连结AF,并延长AF交BC的延长线于点E,使得△ADF与△FCE全等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com