
分析 (1)根据平方差公式可以解答本题;
(2)先化简括号内的式子,再根据二次根式的乘法可以解答本题;
(3)根据完全平方公式可以解答本题;
(4)根据二次根式的乘法和减法可以解答本题.
解答 解:(1)${(\sqrt{3}-2)^{2003}}$${(\sqrt{3}+2)^{2004}}$
=$[(\sqrt{3}-2)(\sqrt{3}+2)]^{2003}•(\sqrt{3}+2)$
=${1}^{2003}×(\sqrt{3}+2)$
=$\sqrt{3}+2$;
(2)($\sqrt{12}$-3$\sqrt{75}$)•$\sqrt{3}$
=$(2\sqrt{3}-15\sqrt{3})•\sqrt{3}$
=$(-13\sqrt{3})•\sqrt{3}$
=-39;
(3)${(\sqrt{2}+\sqrt{5})^2}$-$\sqrt{40}$
=$2+2\sqrt{10}+5-2\sqrt{10}$
=7;
(4)$\frac{{\sqrt{20}+\sqrt{5}}}{{\sqrt{45}}}$-$\sqrt{\frac{1}{3}}$•$\sqrt{6}$
=$\frac{2\sqrt{5}+\sqrt{5}}{3\sqrt{5}}-\sqrt{2}$
=1-$\sqrt{2}$.
点评 本题考查二次根式的化简求值,解题的关键是明确二次根式化简求值的方法.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学八(1)班共50名同学开展了“我为灾区献爱心”捐款活动.小明将捐款情况进行了统计,并绘制成如图的条形统计图.
某中学八(1)班共50名同学开展了“我为灾区献爱心”捐款活动.小明将捐款情况进行了统计,并绘制成如图的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
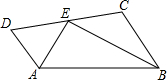 已知,如图,AD∥BC,AE平分∠BAD,BE平分∠ABC,求证:AD+BC=AB.
已知,如图,AD∥BC,AE平分∠BAD,BE平分∠ABC,求证:AD+BC=AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com