
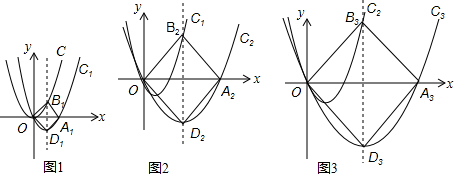
���� ��1������x�ύ��A1���꣬���������ζԽ������ʱ�ʾ��B1�����꣬�����Ӧ�Ľ���ʽ���������Ӧ��b1��ֵ��д��D1�����꣬����y1�Ľ���ʽ�п����a1��ֵ��
��2������x�ύ��A2���꣬���������ζԽ������ʱ�ʾ��B2�����꣬�����Ӧ�Ľ���ʽ���������Ӧ��b2��ֵ��д��D2�����꣬����y2�Ľ���ʽ�п����a2��ֵ��д��������C2�Ľ���ʽ����������ͬ�ķ�����������C3�Ľ���ʽ��
��3���ٸ���ͼ�α任�������ϵ������ó�an=a1=1����B1���꣨1��1����B2���꣨3��3����B3���꣨7��7����Bn���꣨2n-1��2n-1������bn=2��2n-1��=2n+1-2��n��1����д��������Cn����ʽ��
������������C2015��������C2016�Ľ���Ϊ��0��0�����ڽ��������۲�ͼ�εó�y2015��y2016�ĺ���ֵ�Ĵ�С��
��� �⣺��1��y1=0ʱ��a1x��x-b1��=0��
x1=0��x2=b1��
��A1��b1��0����
��������OB1A1D1�ã�OA1=B1D1=b1��
��B1��$\frac{{b}_{1}}{2}$��$\frac{{b}_{1}}{2}$����D1��$\frac{{b}_{1}}{2}$��-$\frac{{b}_{1}}{2}$����
��B1��������c�ϣ���$\frac{{b}_{1}}{2}$=$��\frac{{b}_{1}}{2}��^{2}$��
b1��b1-2��=0��
b1=0�����������⣩��b1=2��
��D1��1��-1����
��D1��1��-1������y1=a1x��x-b1���еã�-1=-a1��
��a1=1��
�ʴ�Ϊ��1��2��
��2��y2=0ʱ��a2x��x-b2��=0��
x1=0��x2=b2��
��A2��b2��0����
��������OB2A2D2�ã�OA2=B2D2=b2��
��B2��$\frac{{b}_{2}}{2}$��$\frac{{b}_{2}}{2}$����
��B2��������c1�ϣ���$\frac{{b}_{2}}{2}$=��$\frac{{b}_{2}}{2}$��2-2��$\frac{{b}_{2}}{2}$��
b2��b2-6��=0��
b2=0�����������⣩��b2=6��
��D2��3��-3����
��D2��3��-3������C2�Ľ���ʽ��-3=3a2��3-6����a2=$\frac{1}{3}$��
��C2�Ľ���ʽ��y2=$\frac{1}{3}$x��x-6��=$\frac{1}{3}$x2-2x��
y3=0ʱ��a3x��x-b3��=0��
x1=0��x2=b3��
��A3��b3��0����
��������OB3A3D3�ã�OA3=B3D3=b3��
��B3��$\frac{{b}_{3}}{2}$��$\frac{{b}_{3}}{2}$����
��B3��������C2�ϣ���$\frac{{b}_{3}}{2}$=$\frac{1}{3}��$��$\frac{{b}_{3}}{2}$��2-2��$\frac{{b}_{3}}{2}$��
b3��b3-18��=0��
b3=0�����������⣩��b3=18��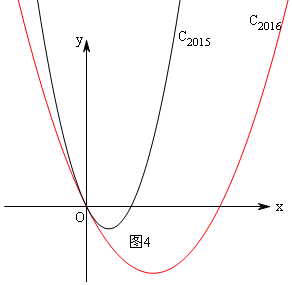
��D3��9��-9����
��D3��9��-9������C3�Ľ���ʽ��-9=9a3��9-18����a3=$\frac{1}{9}$��
��C3�Ľ���ʽ��y3=$\frac{1}{9}$x��x-18��=$\frac{1}{9}{x}^{2}$-2x��
��3����Cn�Ľ���ʽ��yn=$\frac{1}{{3}^{n-1}}$x2-2x��n��1����
��������ɵã�
������C2015�Ľ���ʽΪ��y2015=$\frac{1}{{3}^{2014}}$x2-2x��
������C2016�Ľ���ʽΪ��y2016=$\frac{1}{{3}^{2015}}$x2-2x��
���������ߵĽ���Ϊ��0��0����
��ͼ4����ͼ��ã���x��0ʱ��y2015��y2016��
���� �����Ƕ��κ����뷽�̡������ε��ۺ�Ӧ�ã�������֪ʶ�뷽�̡��������л��ؽ����һ����������һ���ѶȽϴ���������ؼ������ڽ���������ת��Ϊ�������⣬�������������ε��й����ʡ������Ͷ��κ�����֪ʶ����ע���ھ���Ŀ�е�һЩ�����������ʹ�����ԣ��������������x�ύ������?��y=0������㣬�Ѻ�������ת��Ϊ�������⣻�����������ζԽ�������Ҵ�ֱƽ�ֱ�ʾ����ӦB1��B2��B3��Bn�����ꣻ����������������ҽ��������⣬Ҫ�۲�ͼ��д����


 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{3}$ | C�� | 2 | D�� | 2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
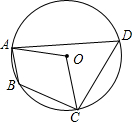 ��ͼ���ı���ABCD�ڽ��ڡ�O������AOC=100�㣬���ABC�Ĵ�СΪ��������
��ͼ���ı���ABCD�ڽ��ڡ�O������AOC=100�㣬���ABC�Ĵ�СΪ��������| A�� | 100�� | B�� | 50�� | C�� | 130�� | D�� | 80�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ������120����������������� | B�� | �����ȱ������� | ||
| C�� | ����ֱ�������� | D�� | ��������ֱ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x+��29-x��=67 | B�� | x+3��29-x��=67 | C�� | 3 x+��30-x��=67 | D�� | x+3��30-x��=67 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ijũ���⽨���䳤������ţ�����ң������ҵ�һ�濿ǽ��ǽ��50m�����м�������ǽ��������ͼ������֪�ƻ��еĽ������Ͽɽ�ǽ���ܳ���Ϊ48m���������䳤������ţ�����ҵ���ռ����������ֵΪ144m2��
ijũ���⽨���䳤������ţ�����ң������ҵ�һ�濿ǽ��ǽ��50m�����м�������ǽ��������ͼ������֪�ƻ��еĽ������Ͽɽ�ǽ���ܳ���Ϊ48m���������䳤������ţ�����ҵ���ռ����������ֵΪ144m2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
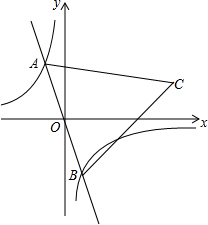 ��ͼ���ڷ���������y=-$\frac{2}{x}$��ͼ������һ����A������AO���ӳ���ͼ�����һ֧�ڵ�B���ڵ�һ��������һ��C������AC=BC������A�˶�ʱ����Cʼ���ں���y=$\frac{k}{x}$��ͼ�����˶�����tan��CAB=2����k��ֵΪ��������
��ͼ���ڷ���������y=-$\frac{2}{x}$��ͼ������һ����A������AO���ӳ���ͼ�����һ֧�ڵ�B���ڵ�һ��������һ��C������AC=BC������A�˶�ʱ����Cʼ���ں���y=$\frac{k}{x}$��ͼ�����˶�����tan��CAB=2����k��ֵΪ��������| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��2 | B�� | m��2 | C�� | 0��m��2 | D�� | m��-2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com