
【题目】如图,抛物线y=ax2+bx﹣2与y轴的交点为A,抛物线的顶点为B(1,﹣3).
(1)求出抛物线的解析式;
(2)点P为x轴上一点,当三角形PAB的周长最小时,求出点P的坐标;
(3)水平移动抛物线,新抛物线的顶点为C,两抛物线的交点为D,当O,C,D在一条直线上时,请直接写出平移的距离.

【答案】(1) y=(x﹣1)2﹣3=x2﹣2x﹣2 (2) P(![]() ,0) (3) 平移距离为2或3
,0) (3) 平移距离为2或3
【解析】
(1)根据题意可得点A的坐标为(0,﹣2),根据顶点坐标为(1,﹣3),可得设抛物线解析式y=a(x﹣1)2﹣3把A点的坐标代入求得a值,即可得抛物线的解析式;(2)当PA+PB最小时,△ABP的周长最小,作A点关于x轴的对称点A'(0,2),连接A'B,用待定系数法求得直线A'B的解析式,直线A'B与x轴的交点坐标即为点P的坐标;(3)设抛物线向右平移m个单位,得到新的抛物线的顶点C(1+m,-3),由此可得新抛物线的解析式,把两个抛物线的解析式联立组成方程组,解方程组求得点D的坐标,再求得直线OC的解析式,因O、C、D三点共线,可得以m为未知数的方程,解方程求得m的值即可.
(1)根据题意得:A(0,﹣2),
设抛物线解析式y=a(x﹣1)2﹣3过点A(0,﹣2),
∴﹣2=a﹣3,
∴a=1,
∴抛物线解析式y=(x﹣1)2﹣3=x2﹣2x﹣2;
(2)∵A(0,﹣2),B(1,﹣3),
∴AB=![]() ,
,
∵△ABP的周长=PA+PB+AB=PA+PB+![]() ,
,
∴当PA+PB最小时,△ABP的周长最小;
作A点关于x轴的对称点A'(0,2),连接A'B,
设直线A'B解析式y=kx+b,
根据题意得:![]() ,
,
解得:k=﹣5,b=2
∴直线A'B的解析式y=﹣5x+2;
当y=0时,x=![]() ,
,
∴P(![]() ,0);
,0);
(3)设向右平移m个单位长度,则所得新的抛物线的顶点C(1+m,-3),
∴平移后抛物线解析式y=(x﹣1﹣m)2﹣3,
∴C(1+m,﹣3),
∴根据题意可得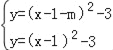 ,
,
∴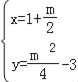 ,
,
∴D(1+![]() ,
,![]() );
);
∵C(1+m,﹣3,),O(0,0),
∴直线CO解析式y=![]() x,
x,
∵O,C,D三点共线,
∴![]() =
=![]() ,
,
解得:m1=0(不合题意舍去),m2=﹣3,m3=2;
∴向右平移2个单位长度,或向左平移3个单位长度,O,C,D三点共线.
∴平移距离为2或3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形ABC中,∠A=110°,求∠B的度数.
例2 等腰三角形ABC中,∠A=40°,求∠B的度数.
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 两地相距30千米,甲骑自行车从
两地相距30千米,甲骑自行车从![]() 地出发前往
地出发前往![]() 地,乙在甲出发1小时后骑摩托车从
地,乙在甲出发1小时后骑摩托车从![]() 地前往
地前往![]() 地,图中的线段
地,图中的线段![]() 和线段
和线段![]() 分别反映了甲和乙所行使的路程
分别反映了甲和乙所行使的路程![]() (千米)与行使时间
(千米)与行使时间![]() (小时)的函数关系。
(小时)的函数关系。

请根据图像所提供的信息回答问题:
(1)乙骑摩托车的速度是每小时20 千米;
(2)两人的相遇地点与B地之间的距离是 千米;
(3)求出甲所行使的路程![]() (千米)与行使时间
(千米)与行使时间![]() (小时)的函数关系式,并写出
(小时)的函数关系式,并写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)某数学兴趣小组想测量商丘电视台电视塔的高度,如图,该小组在商丘电视塔BC前一座楼房楼顶A处所观测到电视塔最高点B的仰角为65°,电视塔最低点C的仰角为30°,楼顶A与电视塔的水平距离AD为90米,求商丘电视塔BC的高度.(结果精确到1米,参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
≈1.73,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上张老师将课本44页第4题进行了改编,图形不变.请你完成下问题.


(1)如图1,∠ACB=∠ADB,BC=BD,求证:△ABC≌△ABD.
(2)如图2,∠CAB=∠DAB,BC=BD,求证:△ABC≌△ABD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解该校七年级学生的身高情况,抽样调查了部分同学身高,将所得数据处理后,制成扇形统计图和频数分布直方图(部分)如下(每组只含最低值不含最高值,身高单位:cm,测量时精确到1cm):
(1)请根据所提供的信息补全频数分布直方图;
(2)样本的中位数落在 (身高值)段中;
(3)如果该校七年级共有500名学生,那么估计全校身高在160cm或160cm以上的七年级学生有 人;
(4)如果上述七年级样本的平均数为157cm,方差为0.8;该校八年级学生身高的平均数为159cm,方差为0.6,那么 学生的身高比较整齐.(填“七年级”或“八年级”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解答下列问题:
在形如ab=N的式子中,我们已经研究过两种情况:
①已知a和b,求N,这是乘方运算;
②已知b和N,求a,这是开方运算.
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫作对数运算.
定义:如果ab=N(a>0.a≠1,N>0),则b叫作以a为底的N的对数,记作b=logaN.
例如:因为23=8,所以log28=3;因为![]() ,所以
,所以![]() .
.
(1)根据定义计算:
①log381= ; ②log33= ;
③log31= ; ④如果logx16=4,那么x= .
(2)设ax=M,ay=N,则logaN=y(a>0,a≠1,M、N均为正数).用logaM,logaN的代数式分别表示logaMN及![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com