
 如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A、B,交y轴负半轴于C,平移CM交x轴于D,交对称轴右边的抛物线于P,使DP=CM,求点P的坐标.
如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A、B,交y轴负半轴于C,平移CM交x轴于D,交对称轴右边的抛物线于P,使DP=CM,求点P的坐标. 分析 先把M点的坐标代入y=-x2+4ax-3得到a=1,则抛物线解析式为y=-x2+4x-3,配成顶点式得到y=-(x-2)2+1,则抛物线的对称轴为直线x=2,易得C(0,-3),根据平移的规律,由于点M向下平移了1个单位,则点C向下平移1个单位,于是得到P点的纵坐标为-4,然后计算当y=-4时的自变量的值即可得到P点坐标.
解答 解:∵M(2,1)在抛物线y=-x2+4ax-3上,
∴-4+8a-3=1,解得a=1,
∴抛物线解析式为y=-x2+4x-3=-(x-2)2+1,抛物线的对称轴为直线x=2,
当x=0时,y=-3,则C(0,-3),
∵平移CM交x轴于D,得到DP,即点M向下平移了1个单位,
∴点C向下平移1个单位,
∴P点的纵坐标为-4,
当y=-4时,-(x-2)2+1=-4,解得x1=2+$\sqrt{5}$,x2=2-$\sqrt{5}$,
∵点P在直线x=2的右侧的抛物线上,
∴P点坐标为(2+$\sqrt{5}$,-4).
点评 本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题可化为解关于x的一元二次方程.也考查了点平移的规律和二次函数图象上点的坐标特征.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:解答题
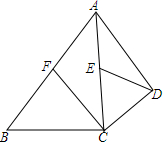 如图,在四边形ABCD中,$\frac{BC}{CD}$=$\frac{3}{2}$,AC平分∠BAD,∠ACB=∠ADC=90°,CF和DE是△ABC、△ACD的中线,求$\frac{CE}{DE}$的值.
如图,在四边形ABCD中,$\frac{BC}{CD}$=$\frac{3}{2}$,AC平分∠BAD,∠ACB=∠ADC=90°,CF和DE是△ABC、△ACD的中线,求$\frac{CE}{DE}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,OA、OB是两条相交的高速公路,C、D是两处村庄,某百货集团响应新农村建设的要求,要在高速路内建一座大型便民超市P,使PC=PD,且P到∠AOB的两边OA、OB的距离相等,那么超市P的位置应选在哪里?
如图所示,OA、OB是两条相交的高速公路,C、D是两处村庄,某百货集团响应新农村建设的要求,要在高速路内建一座大型便民超市P,使PC=PD,且P到∠AOB的两边OA、OB的距离相等,那么超市P的位置应选在哪里?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
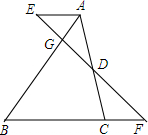 如图,在△ABC中,D是AC的中点,AE∥BC,DE交AB于点G,交BC的延长线于点F,若BG:AG=3:1,BC=10,则线段AE的长为( )
如图,在△ABC中,D是AC的中点,AE∥BC,DE交AB于点G,交BC的延长线于点F,若BG:AG=3:1,BC=10,则线段AE的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com