
【题目】已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.
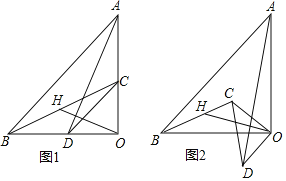
(1)如图1所示,若AB=8,CD=2,求OH的长;
(2)将△COD绕点O旋转一定的角度到图2所示位置时,线段OH与AD有怎样的数量和位置关系,并证明你的结论.
【答案】(1)3;(2)OH=![]() AD,OH⊥AD,证明见解析
AD,OH⊥AD,证明见解析
【解析】
(1)利用勾股定理求出BC,根据直角三角形斜边中线的性质即可解决问题;
(2)如图2中,结论:OH=![]() AD,OH⊥AD.延长OH到E,使得HE=OH(倍长中线构造全等三角形),连接BE,由△BEO≌△ODA即可解决问题.
AD,OH⊥AD.延长OH到E,使得HE=OH(倍长中线构造全等三角形),连接BE,由△BEO≌△ODA即可解决问题.
(1)证明:如图1中,∵△AOB和△COD均为等腰直角三角形,AB=8,CD=2,
∴OB=![]() AB=4
AB=4![]() ,OC=
,OC=![]() CD=
CD=![]() ,
,
∴BC=![]() =
=![]() =
=![]() ,
,

∵在Rt△BOC中,点H为线段BC的中点,
∴OH=![]() BC=
BC=![]() ;
;
(2)解:结论:OH=![]() AD,OH⊥AD,如图2中,延长OH到E,使得HE=OH,连接BE,
AD,OH⊥AD,如图2中,延长OH到E,使得HE=OH,连接BE,
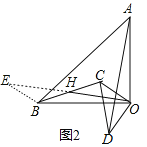
∵点H是BC中点,
∴BH=CH,
∵∠EHB=∠OHC,
∴△BEH≌△COH(SAS),
∴OH=EH,BE=CO,∠EBC=∠BCO,
∴OH=![]() OE,
OE,
∴∠OBE=∠EBC+∠OBC=∠BCO+∠OBC=180°﹣∠BOC,
∵∠AOB=∠COD=90°,
∴∠AOD=180°﹣∠BOC=∠OBE,
∵BE=CO,OC=OD,
∴BE=OD,
∵OB=OA,BE=OD,
∴△BEO≌△ODA(SAS),
∴OE=AD,
∴OH=![]() OE=
OE=![]() AD
AD
∵△BEO≌△ODA,
∴∠EOB=∠DAO
∴∠DAO+∠AOH=∠EOB+∠AOH=90°,
∴OH⊥AD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
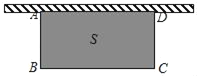
【题目】如图.利用一面墙(墙的长度不限),用20m的篱笆围成一个矩形场地ABCD.设矩形与墙垂直的一边AB=xm,矩形的面积为Sm2.
(1)用含x的式子表示S;
(2)若面积S=48m2,求AB的长;
(3)能围成S=60m2的矩形吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3张扑克牌,分别是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
(1)先后两次抽得的数字分别记为x和y,画出树形图或列表求|x﹣y|≥1的概率.
(2)甲、乙两人做游戏,现有两种方案.A方案:若两次抽得相同花色则甲胜,否则乙胜.B方案:若两次抽得数字和为奇数则甲胜,否则乙胜.请问甲选择哪种方案胜率更高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“网购”的增多,快递业务发展迅速。我市某快递公司今年八月份与十月份完成投递的快递总件数分别为![]() 万件和
万件和![]() 万件,假定该公司每月的投递总件数的增长率相同.
万件,假定该公司每月的投递总件数的增长率相同.
(1)求该快递公司每月的投递总件数的月平均增长率;
(2)由于“双十一”购买量激增,预计11月需投递的快递总件数的增长率将是原来![]() 倍,如果每人每月最多可投递快递
倍,如果每人每月最多可投递快递![]() 万件,该公司现有
万件,该公司现有![]() 名业务员,是否能完成当月投递任务?如果不能,需临时招聘几名业务员?
名业务员,是否能完成当月投递任务?如果不能,需临时招聘几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区的居民用电,按照高峰时段和空闲时段规定了不同的单价.某户5月份高峰时段用电量是空闲时段用电量2倍,6月份高峰时段用电量比5月份高峰时段用电量少50%,结果6月份的用电量和5月份的用电量相等,但6月份的电费却比5月份的电费少25%,求该地区空闲时段民用电的单价比高峰时段的用电单价低的百分率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程ax2+bx+1=0中,b=![]() ;
;
(1)若a=4,求b的值;
(2)若方程ax2+bx+1=0有两个相等的实数根,求方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
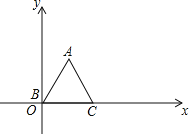
【题目】已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2018次变换后,顶点A的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线y=![]() (x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
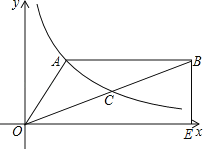
(1)确定k的值: ;
(2)计算△OAB的面积;
(3)若点D(3,b)在双曲线y=![]() (x>0)上,直线AD的解析式为y=mx+n,请直接写出不等式mx+n<
(x>0)上,直线AD的解析式为y=mx+n,请直接写出不等式mx+n<![]() 的解集: .
的解集: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,直径
中,直径![]() 垂直于不过圆心
垂直于不过圆心![]() 的弦
的弦![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 为
为![]() 上一动点,设线段
上一动点,设线段![]() 的长为
的长为![]() .
.
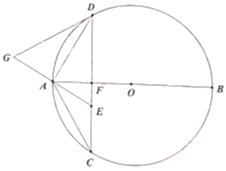
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)设![]() 半径为
半径为![]() ,若点
,若点![]() 为
为![]() 中点,求
中点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com