
 如图,已知A(a,0)、B(0,b),且a、b满足
如图,已知A(a,0)、B(0,b),且a、b满足| a-5 |
 解:(1)△BOD与△AOC全等.理由如下:
解:(1)△BOD与△AOC全等.理由如下:| a-5 |
| a-5 |
|
| 1 |
| 2 |
| 25 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
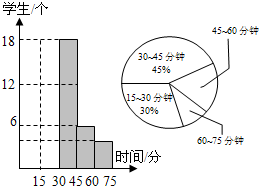 为了了解学校推行素质教育情况,市教育对某个学校七年级学生课外完成作业时间调研后进行了统计,并根据收集的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,解答下面的问题:
为了了解学校推行素质教育情况,市教育对某个学校七年级学生课外完成作业时间调研后进行了统计,并根据收集的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,解答下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:
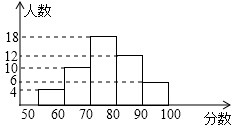 某班进行数学测验,将所得成绩(得分取整数)进行整理后分成5组,并绘制成频数分布直方图,请你结合直方图所提供的信息,回答下列问题:
某班进行数学测验,将所得成绩(得分取整数)进行整理后分成5组,并绘制成频数分布直方图,请你结合直方图所提供的信息,回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com