
【题目】.观察下列算式特点:
①13=12
②13+23=32
③13+23+33=62
④13+23+33+43=102
⑤13+23+33+43+53=152…
(1)请你写出第⑥个算式;
(2)用含n(n为正整数)的式子表示第n个算式;
(3)请用上述规律计算:73+83+93+…+123.
【答案】(1)13+23+33+43+53+63=212;(2)![]() ;(3)5643
;(3)5643
【解析】
(1)利用类比的方法得到第⑥个算式为 13+23+33+43+53+63=212;
(2)同样利用类比的方法得到第n个算式为13+23+33+43+…+n3=![]() ;
;
(3)将73+83+93+…+123转化为(13+23+33+43+…+123)-(13+23+33+43+53+63)后代入总结的规律求解即可.
解:(1)∵①13=12,
②13+23=(1+2)2=32,
③13+23+33=(1+2+3)2=62,
④13+23+33+43=(1+2+3+4)2=102,
⑤13+23+33+43+53=(1+2+3+4+5)2=152,
……,
∴第⑥个算式为13+23+33+43+53+63=(1+2+3+4+5+6)2=212;
(2)第n个算式为13+23+33+43+…+n3=(1+2+3+4+…+n)2=![]() ;
;
(3)73+83+93+…+123
=(13+23+33+43+…+123)-(13+23+33+43+53+63)
=![]()
=6084-441=5643.


科目:初中数学 来源: 题型:
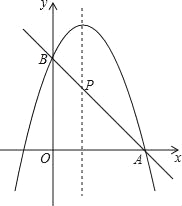
【题目】如图,已知二次函数y=﹣x2+2x+m图象过点A(3,0),与y轴交于点B
(1)求m的值;
(2)若直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线![]() 与X轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒).
与X轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒).

(1)求A,B,C三点的坐标和抛物线的顶点的坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当![]() 时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A、B两种商品,若购进A种商品20件和B种商品15件需380元;若购进A种商品15件和B种商品10件需280元.
(1)求A、B两种商品的进价分别是多少元?
(2)若购进A、B两种商品共100件,总费用不超过900元,问最多能购进A种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
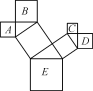
【题目】如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,则最大正方形E的面积是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
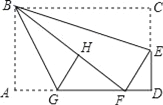
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=![]() S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.
其中正确的是__.(把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,且ABCD的周长为40,则ABCD的面积为( )
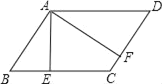
A. 24B. 36C. 40D. 48
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com