
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:选择题
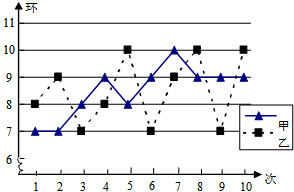 在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )
在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
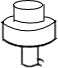 如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间x变化的函数图象最接近实际情况的是( )
如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间x变化的函数图象最接近实际情况的是( )| A. | 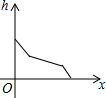 | B. | 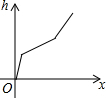 | C. | 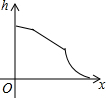 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
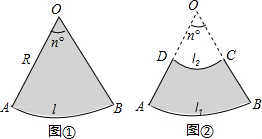
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
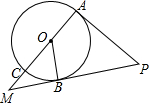 如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-$\frac{3}{x}$ | B. | y=$\frac{-3}{2x}$ | C. | y=$\frac{1}{x-1}$ | D. | 3xy=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com