
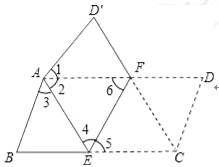
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.

(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
【答案】见试题解析
【解析】试题分析:(1)根据平行四边形的性质及折叠的性质我们可以得到∠B=∠D′,AB=AD′,∠1=∠3,从而利用ASA判定△ABE≌△AD′F;
(2)四边形AECF是菱形,我们可以运用菱形的判定,有一组邻边相等的平行四边形是菱形来进行验证.
试题解析:(1)证明:由折叠可知:∠D=∠D′,CD=AD′,
∠C=∠D′AE.
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,∠C=∠BA D.
∴∠B=∠D′,AB=AD′,∠D′AE=∠BAD,
即∠1+∠2=∠2+∠3.
∴∠1=∠3.
又∠B=∠D′,AB=AD′
∴△ABE≌△AD′F(ASA).
(2)解:四边形AECF是菱形.
证明:由折叠可知:AE=EC,∠4=∠5.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠5=∠6.
∴∠4=∠6.
∴AF=AE.
∵AE=EC,
∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形.
又∵AF=AE,
∴平行四边形AECF是菱形.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.两条射线所组成的图形叫做角
B.一条直线可以看成一个平角
C.角的两边越长,角就越大
D.角的大小和它的度数大小是一致的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c是三角形的三条边,则|a+b﹣c|﹣|c﹣a﹣b|的化简结果为( )
A. 0 B. 2a+2b C. 2c D. 2a+2b﹣2c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三边分别是a,b,c,试化简|a﹣b﹣c|+|b﹣c+a|﹣|c﹣b﹣a|值为( )
A. ﹣a+b+c.B. 3a+b﹣3c.C. ﹣a+b-c.D. ﹣3a﹣b+3c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)将下列各数填在相应的集合里.
﹣(﹣2.5),(﹣1)2,﹣|﹣2|,﹣22,0, ![]() ,﹣1.5;
,﹣1.5;
正数集合{ …}
分数集合{ …}
(2)把表示上面各数的点画在数轴上,再按从小到大的顺序,用“<“号把这些数连接起来.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过反比例函数y= ![]() (x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2 , 比较它们的大小,可得( )
(x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2 , 比较它们的大小,可得( ) 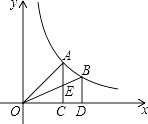
A.S1>S2
B.S1=S2
C.Sl<S2
D.大小关系不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD中,AB=CD=10cm,BC=AD=8cm,动点P以1cm/s的速度从A点出发,沿A→B→C→D路线运动到点D停止,动点Q以2cm/s的速度从D点出发,沿D→C→B→A路线运动到点A停止,两点同时出发,6s后P、Q同时改变速度,点P的速度为2cm/s,点Q的速度为1cm/s, 当点Q出发_____秒时,点P与点Q在运动路线上相距的路程为26cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com